Một con thuyền rời bến ${O(0,0)}$ trên một bờ sông, luôn đi với vận tốc không đổi 20 dặm/giờ hướng về bến ${A(1000,0)}$ (phía đông của ${O}$ ); đồng thời nước sông chảy ngược lên phía bắc với tốc độ 5 dặm/giờ

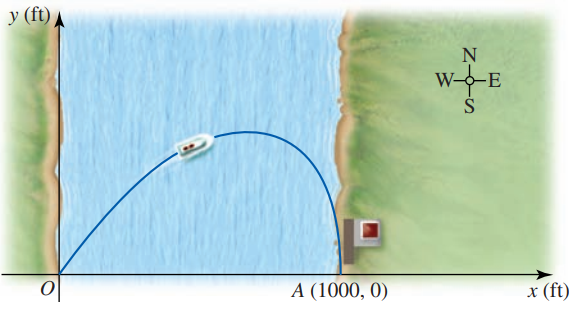
Một con thuyền rời bến ${O(0,0)}$ trên một bờ sông, luôn đi với vận tốc không đổi 20 dặm/giờ hướng về bến ${A(1000,0)}$ (phía đông của ${O}$ ); đồng thời nước sông chảy ngược lên phía bắc với tốc độ 5 dặm/giờ. Người ta cho rằng đường đi của thuyền là $y=500\left[ {{\left( \dfrac{1000-x}{1000} \right)}^{3/4}}-{{\left( \dfrac{1000-x}{1000} \right)}^{5/4}} \right],\quad 0\le x\le 1000$

Tìm độ lệch bắc lớn nhất mà thuyền đạt được trong suốt hành trình.

Lời giải

Đặt $u=\dfrac{1000-x}{1000},\quad \text{ th }\grave{\mathrm{i}}\text{ }0\le u\le 1,\quad x=1000(1-u).$

Khi đó $y(u)=500\left( {{u}^{3/4}}-{{u}^{5/4}} \right).$

Tính đạo hàm theo ${u}$ : $500\left( \dfrac{3}{4}{{u}^{-1/4}}-\dfrac{5}{4}{{u}^{1/4}} \right)=500\cdot \dfrac{1}{4}{{u}^{-1/4}}(3-5u)$

Vì ${u^{-1 / 4}{>}0}$ trên ${(0,1]}$, ta chỉ cần giải $3-5u=0\Rightarrow u=\dfrac{3}{5}=0,6$

Lập bảng xét dấu ta có

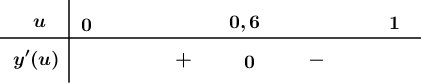
Suy ra $y(u)$ đạt điểm cực đại tại $u=0,6$

Chuyển lại thành ${x}$ và tính ${{y}_{C}}$

– Tương ứng $x=1000(1-u)=1000\cdot 0,4=400$.

– Độ lệch bắc cực đại là ${{y}_{C}}=500\left( {{(0,6)}^{3/4}}-{{(0,6)}^{5/4}} \right)\approx 500(0,6817-0,5286)\approx 76,6$

Do đó giá trị ${{y}_{C}}\approx 76,6$ tại ${x=400}$

Kết luận:

Trong suốt hành trình, con thuyền bị dòng nước đẩy lệch về phía bắc cực đại khoảng

76,6 (đơn vị chiều dài) khi nó đã đi được ${x=400}$ (đơn vị tương ứng) về phía đông.