Một bể ban đầu chứa 10 gal dung dịch muối với 2 lb muối. Dung dịch vào có nồng độ ${1.5 {lb} / {gal}}$ chảy vào với tốc độ ${3 {gal} /}$ phút, và hỗn hợp trong bể chảy ra với tốc độ ${4 {gal} /}$ phút. Người ta cho biết lượng muối trong bể sau ${t}$ phút là ${x}$ (pound), với
$x=f(t)=1,5(10-t)-0,0013{{(10-t)}^{4}},\quad 0\le t\le 10.$
Hỏi lượng muối tối đa có thể có trong bể tại một thời điểm nào đó là bao nhiêu? (làm tròn kết quả đến hàng phần trăm)

Lời giải
Trả lời: 7,43
Ta có công thức lượng muối ${x}$ (pound) trong bể sau ${t}$ phút:
$x(t)=1,5(10-t)-0,0013{{(10-t)}^{4}};\quad 0\le t\le 10$
Đặt ${u=10-t}$. Khi ${t}$ chạy từ 0 đến 10 thì ${u}$ chạy từ 10 xuống 0.
Khi đó $x=1,5u-0,0013{{u}^{4}};\quad 0\le u\le 10$
Tính đạo hàm theo ${u}$ ta được: $1,5-0,0013\cdot 4{{u}^{3}}=1,5-0,0052{{u}^{3}}$
Xét $1,5-0,0052{{u}^{3}}=0\Rightarrow {{u}^{3}}=\dfrac{1,5}{0,0052}\approx 288,46\Rightarrow u\approx \sqrt[3]{288,46}\approx 6,62$
Lập bảng xét dấu ta được:
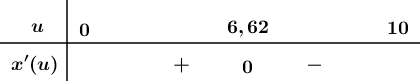
Suy ra tại $u\approx 6,62$ : ${{x}_{C}}=1,5\cdot 6,62-0,0013{{(6,62)}^{4}}\approx 9,93-2,50\approx 7,43lb.$
Lượng muối trong bể đạt tối đa khoảng 7,43 lb tại thời điểm $t\approx 3,38$ phút kể từ lúc bắt đầu.
