Định mức cầu mỗi tháng của đồng hồ đeo tay Peget phụ thuộc vào giá đơn vị ${p}$ theo phương trình cầu $p=\dfrac{50}{0.01{{x}^{2}}+1},\quad 0\le x\le 20$ trong đó ${p}$ tính bằng đô la và ${x}$ tính bằng nghìn chiếc. Hỏi nhà sản xuất phải bán bao nhiêu nghìn chiếc để doanh thu ${R=p x}$ đạt cực đại?
Lời giải
Trả lời: 10
Doanh thu ${R(x)}$ là $R(x)=p(x)x=\dfrac{50x}{0,01{{x}^{2}}+1}$
Tính đạo hàm ${R^{\prime}(x)}$
${{R}^{\prime }}(x)=\dfrac{\left( 0,01{{x}^{2}}+1 \right)\cdot 50-50x\cdot (0,02x)}{{{\left( 0,01{{x}^{2}}+1 \right)}^{2}}}=\dfrac{50\left( 0,01{{x}^{2}}+1-0,02{{x}^{2}} \right)}{{{\left( 0,01{{x}^{2}}+1 \right)}^{2}}}=\dfrac{50\left( 1-0,01{{x}^{2}} \right)}{{{\left( 0,01{{x}^{2}}+1 \right)}^{2}}};0\le x\le 20$
Giải ${R^{\prime}(x)=0}$ : $1-0,01{{x}^{2}}=0\Rightarrow {{x}^{2}}=100\Rightarrow x=10$
Có bảng xét dấu:
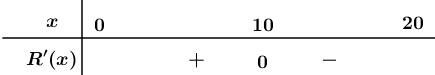
Suy ra được hàm số đạt cực đại tại $x=10$
Giá trị cực đại là ${R(10)=250}$.
