Vận tốc trung bình của dòng xe trên đoạn đường 124 từ 6#A.M. đến 10#A.M. được xấp xỉ bởi $f(t)=20t-40\sqrt{t}+50,\quad 0\le t\le 4$ trong đó ${t}$ tính bằng giờ kể từ $6$ A.M. và ${f(t)}$ tính bằng km/giờ. Hỏi vào thời điểm mấy giờ trong buổi sáng (giữa 6#A.M. và 10#A.M.) thì vận tốc trung bình thấp nhất?
Lời giải
Trả lời: 7
Tính đạo hàm ${{f}^{\prime }}(t)=20-40\cdot \dfrac{1}{2\sqrt{t}}=20-\dfrac{20}{\sqrt{t}}$
Xét ${f^{\prime}(t)=0}$ : $20-\dfrac{20}{\sqrt{t}}=0\Rightarrow \dfrac{20}{\sqrt{t}}=20\Rightarrow \sqrt{t}=1\Rightarrow t=1$
Lập bảng xét dấu ta được:
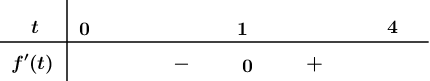
Suy ra vận tốc trung bình thấp nhất 30 mph xảy ra vào 7:00#A.M. ${(t=1)}$.
