Giả sử tổng chi phí sản xuất $x$ $\left( 0\le x\le 50 \right)$ đơn vị sản phẩm $A$ mỗi ngày tại một nhà máy được cho bởi công thức $C\left( x \right)=\dfrac{{{x}^{2}}}{4}+3x+400$ (nghìn đồng) và toàn bộ chúng được bán hết với giá $\left( 900-6x \right)$ nghìn đồng một sản phẩm. Tìm mức sản lượng (đó là số lượng sản phẩm được sản xuất) để chi phí trung bình tính trên mỗi đơn vị sản phẩm là đạt cực tiểu.
Lời giải
Đáp án: $40$.
Kí hiệu $\bar{C}\left( x \right)$ là chi phí trung bình tính trên mỗi đơn vị sản phẩm.
Ta có $\bar{C}\left( x \right)=\dfrac{C\left( x \right)}{x}=\dfrac{x}{4}+3+\dfrac{400}{x}$.
Đạo hàm: ${\bar{C}}’\left( x \right)=\dfrac{{{x}^{2}}-1600}{4{{x}^{2}}}=0\Leftrightarrow x=40$ (vì $0\le x\le 50$ ).
Bảng biến thiên như sau
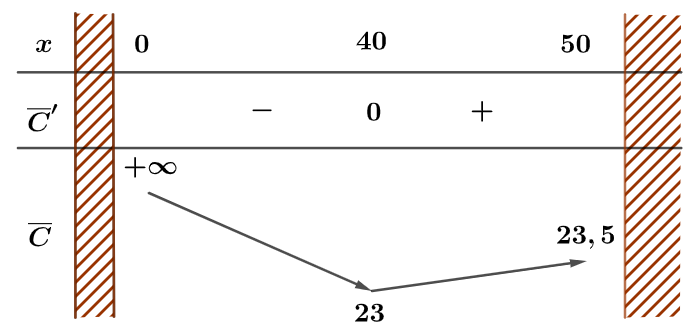
Vậy mức sản lượng $x=40$.
