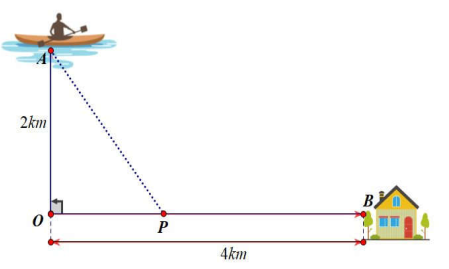
Anh Ba đang trên chiếc thuyền tại vị trí A cách bờ sông $2km$, anh dự định chèo thuyền vào bờ và tiếp tục chạy bộ theo một đường thẳng để đến một địa điểm B tọa lạc ven bờ sông, B cách vị trí O trên bờ gần với thuyền nhất là $4km$ (hình vẽ). Biết rằng anh Ba chèo thuyền với vận tốc $6m/h$ và chạy bộ trên bờ với vận tốc $10km/h$. Khoảng thời gian ngắn nhất để anh Ba từ vị trí xuất phát đến được điểm B là bao nhiêu phút?
Lời giải
Trả lời: 40
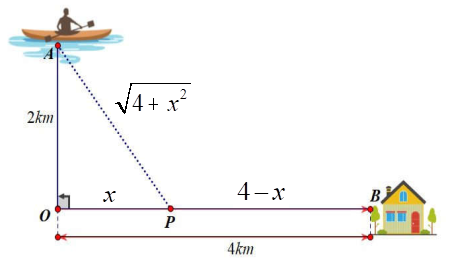
Đặt $OP=x\left( 0{<}x{<}4 \right)\Rightarrow BP=4-x;AP=\sqrt{4+{{x}^{2}}}$.
Khoảng thời gian để anh Ba từ vị trí xuất phát đến được điểm B là:
${{t}_{\left( x \right)}}={{t}_{AP}}+{{t}_{PB}}=\dfrac{\sqrt{4+{{x}^{2}}}}{6}+\dfrac{4-x}{10}\left( h \right).\Rightarrow {{{t}’}_{\left( x \right)}}=\dfrac{x}{6\sqrt{4+{{x}^{2}}}}-\dfrac{1}{10}$.
${{{t}’}_{\left( x \right)}}=0\Leftrightarrow \dfrac{x}{6\sqrt{4+{{x}^{2}}}}-\dfrac{1}{10}=0\Leftrightarrow 3\sqrt{4+{{x}^{2}}}=5x\Leftrightarrow \left\{ \begin{array}{l}
0{<}x{<}4 \\
4{{x}^{2}}=9 \\
\end{array} \right.\Leftrightarrow x=\dfrac{3}{2}.$
BBT:
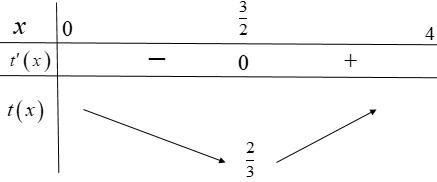
Từ BBT suy ra khoảng thời gian ngắn nhất để anh Ba từ vị trí xuất phát đến được điểm B là:
${{t}_{\min }}=\dfrac{2}{3}\left( h \right)=\dfrac{2}{3}.60=40$ (phút).
