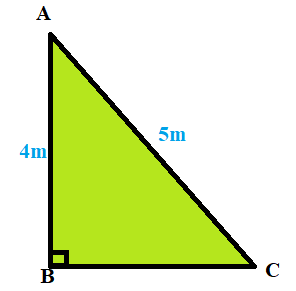
Chào đón năm mới $2025$, Thành phố trang trí đèn led biểu tượng hình chữ $V$ được ghép từ các thanh $AB=4m$, $AC=5m$ sao cho tam giác $ABC$ vuông tại $B$. Để tăng hiệu ứng, các kỹ sư đã thiết kế một chuỗi led chạy từ $B$ xuống $A$ với vận tốc $4$ $\text{m/}$ phút và một chuỗi led chạy từ $A$ lên $C$ với vận tốc $10$ $\text{m/}$ phút. Sau khi đóng nguồn điện thì cả hai chuỗi led đồng thời xuất phát. Hỏi sau bao nhiêu giây từ thời điểm đóng nguồn thì khoảng cách giữa hai điểm sáng đầu tiên của hai chuỗi led là nhỏ nhất ?
Lời giải
Trả lời: 16
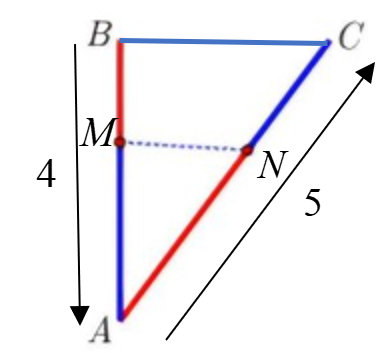
Gọi $x$ (phút) là khoảng thời gian cả hai chuỗi led đồng thời xuất phát đến $M$ và $N$ là hai điểm sáng đầu tiên
$\Rightarrow \left\{ \begin{array}{l}
BM=4x \\
AN=10x \\
\end{array} \right.$ $\Rightarrow AM=4-4x$ với $0\le x\le 4$
Xét tam giác $ABC$ vuông tại $B$ $\Rightarrow \cos \widehat{MAN}=\dfrac{AB}{AC}=\dfrac{4}{5}$
Xét tam giác $AMN$ ta có : $M{{N}^{2}}=A{{M}^{2}}+A{{N}^{2}}-2AM.AN.\cos \widehat{MAN}$
$M{{N}^{2}}={{\left( 4-4x \right)}^{2}}+{{\left( 10x \right)}^{2}}-2.\left( 4-4x \right).10x.\dfrac{4}{5}$ $=180{{x}^{2}}-96x+16=f\left( x \right)$
Để khoảng cách giữa hai điểm sáng đầu tiên của hai chuỗi led nhỏ nhất $\Leftrightarrow M{{N}_{\min }}\Leftrightarrow M{{N}^{2}}_{\min }$
Xét $f\left( x \right)=180{{x}^{2}}-96x+16$ với $x\in \left[ 0;4 \right]$
${f}’\left( x \right)=360x-96=0\Leftrightarrow$ $x=\dfrac{4}{15}$ $\Rightarrow M{{N}^{2}}$ đạt giá trị nhỏ nhất $\Leftrightarrow x=\dfrac{4}{15}$ (phút) $=16$ (giây)
Vậy sau 16 giây thì hai điểm sáng đầu tiên của chuỗi led có khoảng cách nhỏ nhất.
