Doanh số bán hàng của một loại sản phẩm (chục triệu đồng) trong một phiên livestream bán hàng kéo dài sáu giờ theo quy luật hàm số $f(t)=\dfrac{3t}{{{e}^{\dfrac{t}{2}}}},0\le t\le 6$ trong đó thời gian $t$ được tính bằng giờ kể từ khi bắt đầu livestream

Doanh số bán hàng của một loại sản phẩm (chục triệu đồng) trong một phiên livestream bán hàng kéo dài sáu giờ theo quy luật hàm số $f(t)=\dfrac{3t}{{{e}^{\dfrac{t}{2}}}},0\le t\le 6$ trong đó thời gian $t$ được tính bằng giờ kể từ khi bắt đầu livestream.

Khi đó, đạo hàm $f\prime (t)$ sẽ biểu thị tốc độ bán hàng. Hỏi sau bao nhiêu giờ kể từ khi bắt đầu phiên livestream thì doanh số bán hàng là lớn nhất?

Lời giải

Trả lời: 2

Ta có: $f\prime (t)=\dfrac{6-3t}{2{{e}^{\dfrac{t}{2}}}}$

$f\prime (t)=0\Leftrightarrow 6-3t=0\Leftrightarrow t=2$

Ta có bảng biến thiên với $t\in \left[ 0;6 \right]$ :

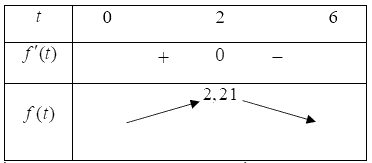
Vậy sau 2 giờ kể từ khi bắt đầu phiên livestream thì doanh số bán hàng là lớn nhất.