Bài toán gốc
Cho hàm số $y= f(x) = x^3+5x^2+7x+7$ đạt cực tiểu tại $x = a$, cực đại tại $x = b$. Khi đó $3a + 6b$ bằng bao nhiêu?
Đáp án: -17
Lời giải: Ta có tập xác định $D = \mathbb{R}$.
Đạo hàm $y^{\prime} = 3x^2+10x+7$.
Cho $y^{\prime}= 0 \Leftrightarrow \left[\begin{array}{l} x_1=-\dfrac{7}{3}\\ x_2=-1.\end{array}\right.$
Ta có bảng biến thiên
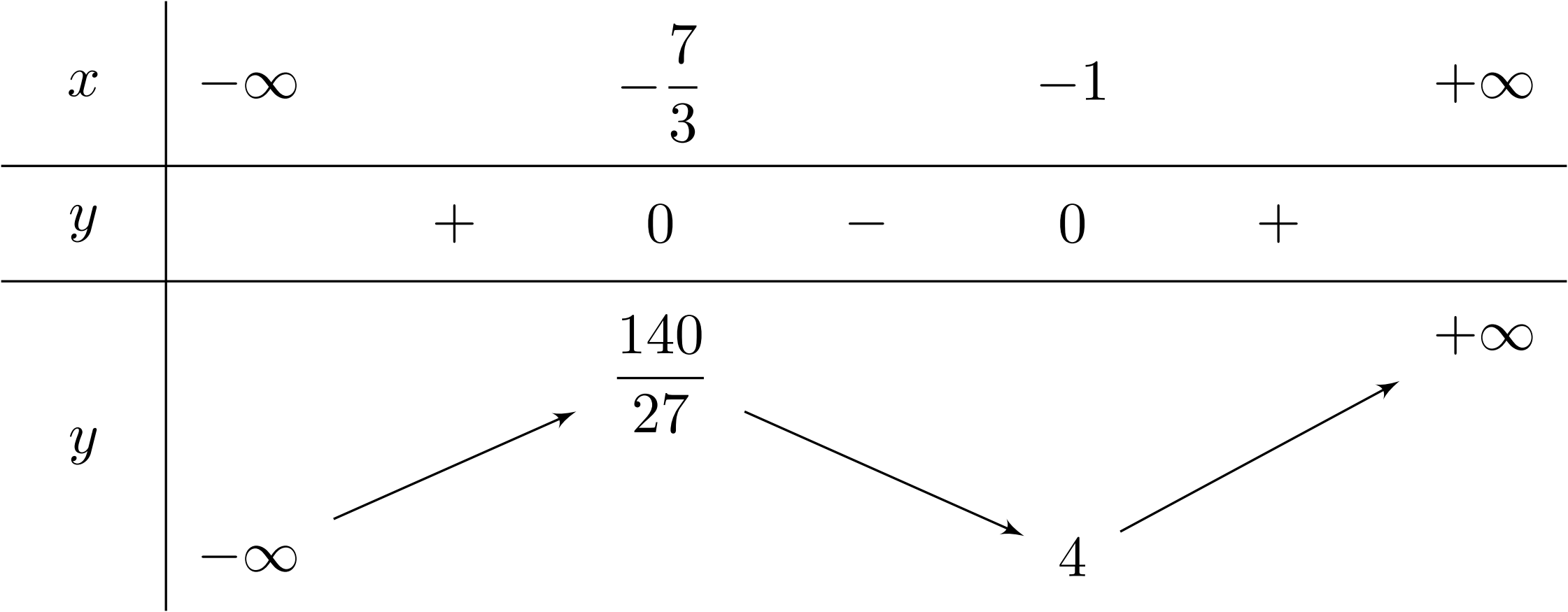
Dựa vào BBT, ta có $3a + 6b = 3 \left(-1\right) + 6 \left(-\dfrac{7}{3}\right) = -17.$
Phân tích và Phương pháp giải
Đây là dạng bài toán tìm tọa độ các điểm cực trị (cực đại và cực tiểu) của hàm số bậc ba. Phương pháp giải là tính đạo hàm bậc nhất ($y’$), giải phương trình $y’=0$ để tìm các điểm tới hạn. Sau đó, dựa vào dấu của hệ số bậc ba (hoặc bảng biến thiên/dấu của $y’$) để xác định điểm nào là cực đại, điểm nào là cực tiểu, rồi thay thế các giá trị $x$ tương ứng vào biểu thức yêu cầu.
Bài toán tương tự
Cho hàm số $y= x^3 – 3x^2 – 9x + 2$ đạt cực tiểu tại $x = a$, cực đại tại $x = b$. Khi đó giá trị của biểu thức $5a + 2b$ bằng bao nhiêu?
Đáp án: 13
Lời giải ngắn gọn:
Ta có đạo hàm $y’ = 3x^2 – 6x – 9$.
Cho $y’=0 \Leftrightarrow 3(x^2 – 2x – 3) = 0 \Leftrightarrow (x+1)(x-3) = 0$. Các điểm tới hạn là $x_1 = -1$ và $x_2 = 3$.
Vì hệ số của $x^3$ là $1 > 0$, hàm số đạt cực đại tại điểm $x$ nhỏ hơn và cực tiểu tại điểm $x$ lớn hơn.
Cực đại $b = -1$.
Cực tiểu $a = 3$.
Giá trị cần tìm là $5a + 2b = 5(3) + 2(-1) = 15 – 2 = 13.
