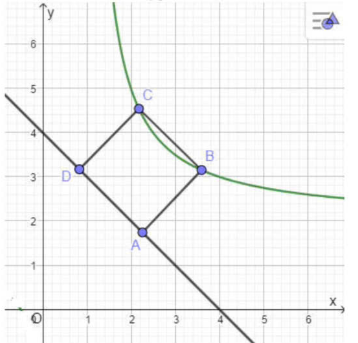
Trong một công viên có một hồ nước và một đường đi lát gạch hoa. Thiết lập hệ trục $Oxy$ như hình vẽ dưới, kiến trúc sư thấy rằng bờ hồ có thể coi như một nhánh của đồ thị hàm số $y=\dfrac{2x+1}{x-1}$ và đường đi khi đó ứng với đường thẳng $\left( d \right):y=-x+4$. Để đảm bảo ánh sáng, kiến trúc sư muốn đặt 2 cột đèn trên bờ hồ và 2 cột đèn trên đường đi sao cho 4 cột đèn này tạo thành một hình vuông. Tính khoảng cách giữa hai cột đèn trên bờ hồ (làm tròn đến hàng phần trăm).
Lời giải
Đáp án: $1,92$.
Gọi $\left( {{d}_{1}} \right):y=-x+m$ (với $m{>}4$ ) song song với $\left( d \right):y=-x+4$ và cắt $(C):y=\dfrac{2x+1}{x-1}$ tại hai điểm phân biệt $B,C$ ( ${{x}_{B}};{{x}_{C}}{>}1$ )
Phương trình hoành độ giao điểm của $\left( {{d}_{1}} \right)$ và $(C)$ : $\dfrac{2x+1}{x-1}=-x+m\Leftrightarrow {{x}^{2}}+\left( 1-m \right)x+m+1=0.$
$\Delta ={{m}^{2}}-6m-3{>}0\Leftrightarrow \left[ \begin{array}{l}
m{>}3+2\sqrt{3} \\
m{<}3-2\sqrt{3} \\
\end{array} \right.\Leftrightarrow m{>}3+2\sqrt{3}$ (vì $m{>}4$ ) (1)
Khi đó ta có: $\left\{ \begin{array}{l}
{{x}_{C}}+{{x}_{B}}=m-1 \\
{{x}_{C}}.{{x}_{B}}=m+1 \\
\end{array} \right.$
Suy ra: $CB=\sqrt{{{\left( {{x}_{B}}-{{x}_{C}} \right)}^{2}}+{{\left( {{y}_{B}}-{{y}_{C}} \right)}^{2}}}=\sqrt{{{\left( {{x}_{B}}-{{x}_{C}} \right)}^{2}}+{{\left( -{{x}_{B}}+m+{{x}_{C}}-m \right)}^{2}}}=\sqrt{2{{\left( {{x}_{B}}-{{x}_{C}} \right)}^{2}}}$
$\Rightarrow C{{B}^{2}}=2{{\left( {{x}_{B}}-{{x}_{C}} \right)}^{2}}=2{{\left( {{x}_{B}}+{{x}_{C}} \right)}^{2}}-8{{x}_{B}}.{{x}_{C}}=2{{m}^{2}}-12m-6$
Mặt khác chọn $I\left( 0;4 \right)\in \left( d \right)$, ta có khoảng cách giữa hai đường thẳng $\left( d \right);\left( {{d}_{1}} \right)$ bằng $AB=d\left( I;\left( {{d}_{1}} \right) \right)=\dfrac{\left| 4-m \right|}{\sqrt{2}}=\dfrac{m-4}{\sqrt{2}}$
Để $ABCD$ là hình vuông thì $A{{B}^{2}}=B{{C}^{2}}\Leftrightarrow \dfrac{{{\left( m-4 \right)}^{2}}}{2}=2{{m}^{2}}-12m-6\Leftrightarrow m=\dfrac{8\pm 2\sqrt{37}}{3}$
Kết hợp điều kiện (1) suy ra $m=\dfrac{8+2\sqrt{37}}{3}$
Vậy khoảng cách giữa hai cột đèn bên bờ hồ bằng $\dfrac{\dfrac{8+2\sqrt{37}}{3}-4}{\sqrt{2}}\approx 1,92.$
