Một doanh nghiệp dự định sản xuất không quá 400 sản phẩm. Nếu doanh nghiệp sản xuất $x$ sản phẩm $(1\le x\le 400)$ thì doanh thu nhận được khi bán hết số sản phẩm là $F\left( x \right)={{x}^{3}}-1999{{x}^{2}}+1001000x+250000$ ( đồng).Trong đó, chi phí vận hành máy móc cho mỗi sản phẩm là $G(x)=\dfrac{100000x}{\dfrac{3}{2}x+1}$ đồng. Tổng chi phí mua nguyên vật liệu là $H(x)=2{{x}^{3}}+100000x-50000$ ( đồng) nhưng do doanh nghiệp mua với số lượng lớn nên được giảm 1
Lời giải
Đáp án: 253
Ta có chi phí
$H(200)=35950000$
$H(x-200)=2{{(x-200)}^{3}}+100000(x-200)-50000,v\acute{i}i400\ge x{>}200$
Ta có lợi nhuận thu được tính như sau:
$f(x)=\left\{ \begin{array}{l}
{{x}^{3}}-1999{{x}^{2}}+1001000x+250000-\dfrac{100000{{x}^{2}}}{\dfrac{3}{2}x+1}-\dfrac{99}{100}(2{{x}^{3}}+100000x-50000),\text{khi}0\le x\le 200 \\
{{x}^{3}}-1999{{x}^{2}}+1001000x+250000-\dfrac{100000{{x}^{2}}}{\dfrac{3}{2}x+1}-\dfrac{99}{100}H\left( 200 \right)-\dfrac{98}{100}H(x-200),\text{khi}200{<}x\le 400 \\
\end{array} \right.$
*. Xét trường hợp khi $0\le x\le 200$
$f(x)=-0,98{{x}^{3}}-1999{{x}^{2}}+902000x+299500-\dfrac{200000{{x}^{2}}}{3x+2}$
$\Rightarrow f'(x)=\dfrac{-26,46{{x}^{4}}-36017,28{{x}^{3}}+8070912,24{{x}^{2}}+10080008x+3608000}{{{(3x+2)}^{2}}}$
$\Rightarrow f’\left( x \right)=0\Leftrightarrow x\approx 196,98$
BBT:
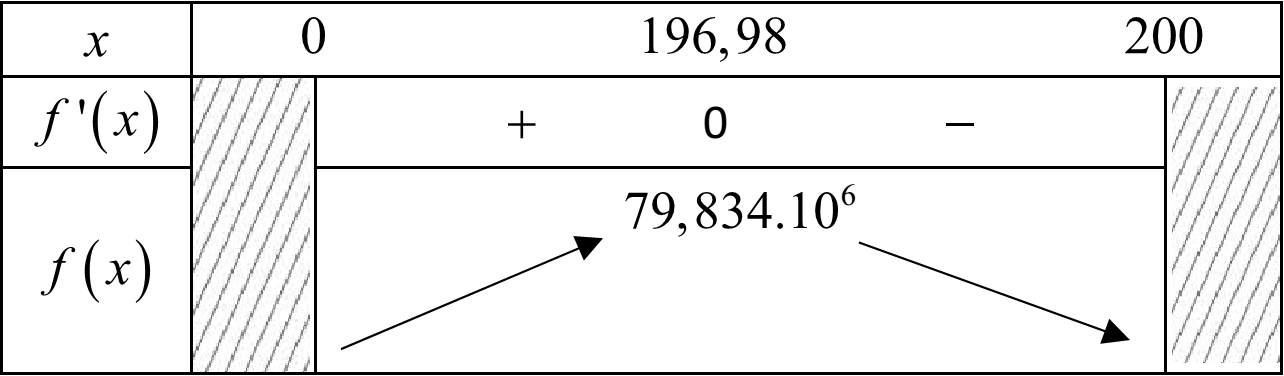
*. Xét trường hợp khi $200{<}x\le 400$
$f(x)=-0,96{{x}^{3}}-823{{x}^{2}}+667800x-11500-\dfrac{200000{{x}^{2}}}{3x+2},200{<}x\le 400$
$\Rightarrow {f}’\left( x \right)=-2,88{{x}^{2}}-1646x+667800-\dfrac{600000{{x}^{2}}+800000x}{{{\left( 3x+2 \right)}^{2}}}$
$\Rightarrow {f}’\left( x \right)=0\Leftrightarrow x\approx 253,11$
BBT:
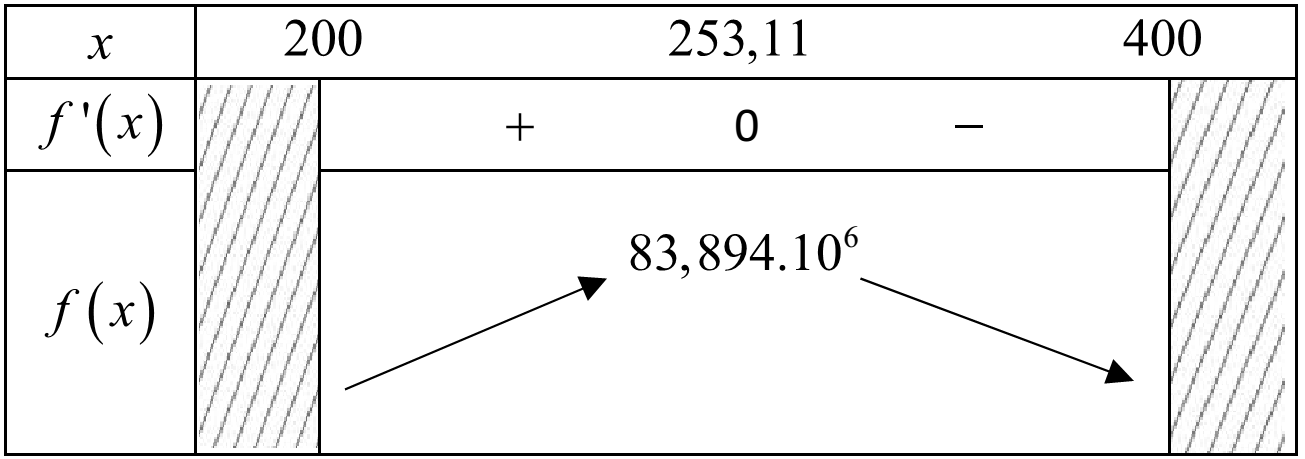
Vì số sản phẩm sản xuất được là số tự nhiên, từ BBT trên ta so sánh $f\left( 253 \right)$ và $f\left( 254 \right)$
Ta có: $f\left( 253 \right)\approx 83893648,05$ và $f\left( 254 \right)\approx 83892445,32$
Vậy doanh nghiệp cần sản xuất 253 sản phẩm thì lợi nhuận là lớn nhất
