Một doanh nghiệp dự định sản xuất không quá $300$ sản phầm

Một doanh nghiệp dự định sản xuất không quá $300$ sản phầm. Nếu doanh nghiệp sản xuất $x$ sản phẩm $\left( 1\le x\le 300 \right)$ thì doanh thu nhận được khi bán hết số sản phẩm đó là $F\left( x \right)=-2{{x}^{2}}+1312x$ (nghìn đồng), trong khi chi phí sản xuất bình quân cho một sản phẩm là $G\left( x \right)={{x}^{2}}-77x+1000+\dfrac{40000}{x}$ (nghìn đồng). Lợi nhuận thu được của doanh nghiệp (tính theo đơn vị triệu đồng) đạt giá trị lớn nhất bằng bao nhiêu (làm tròn kết quả đến hàng đơn vị).

Lời giải

Đáp án: 38.

Chi phí sản xuất cho $x$ sản phẩm là $xG\left( x \right)={{x}^{3}}-77{{x}^{2}}+1000x+40000$ (nghìn đồng).

Lợi nhuận thu được của doanh nghiệp:

$h\left( x \right)=-2{{x}^{2}}+1312x-\left( {{x}^{3}}-77{{x}^{2}}+1000x+40000 \right)=-{{x}^{3}}+75{{x}^{2}}+312x-40000$ (nghìn đồng).

Ta có: $h’\left( x \right)=-3{{x}^{2}}+150x+312$.

Xét $h’\left( x \right)=0\Leftrightarrow \left[ \begin{array}{l}

x=52 \\

x=-2 \\

\end{array} \right.$.

Bảng biến thiên:

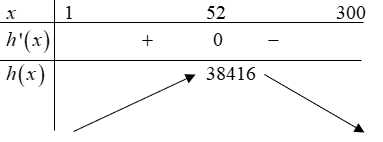
Vậy lợi nhuận lớn nhất của doanh nghiệp khoảng $38$ triệu đồng.