Câu hỏi:
Tính \(\smallint {e^{{{\cos }^2}x}}\sin 2xdx\) bằng
Lời Giải:
Đây là các câu trắc nghiệm về NGUYÊN HÀM mức độ 1,2 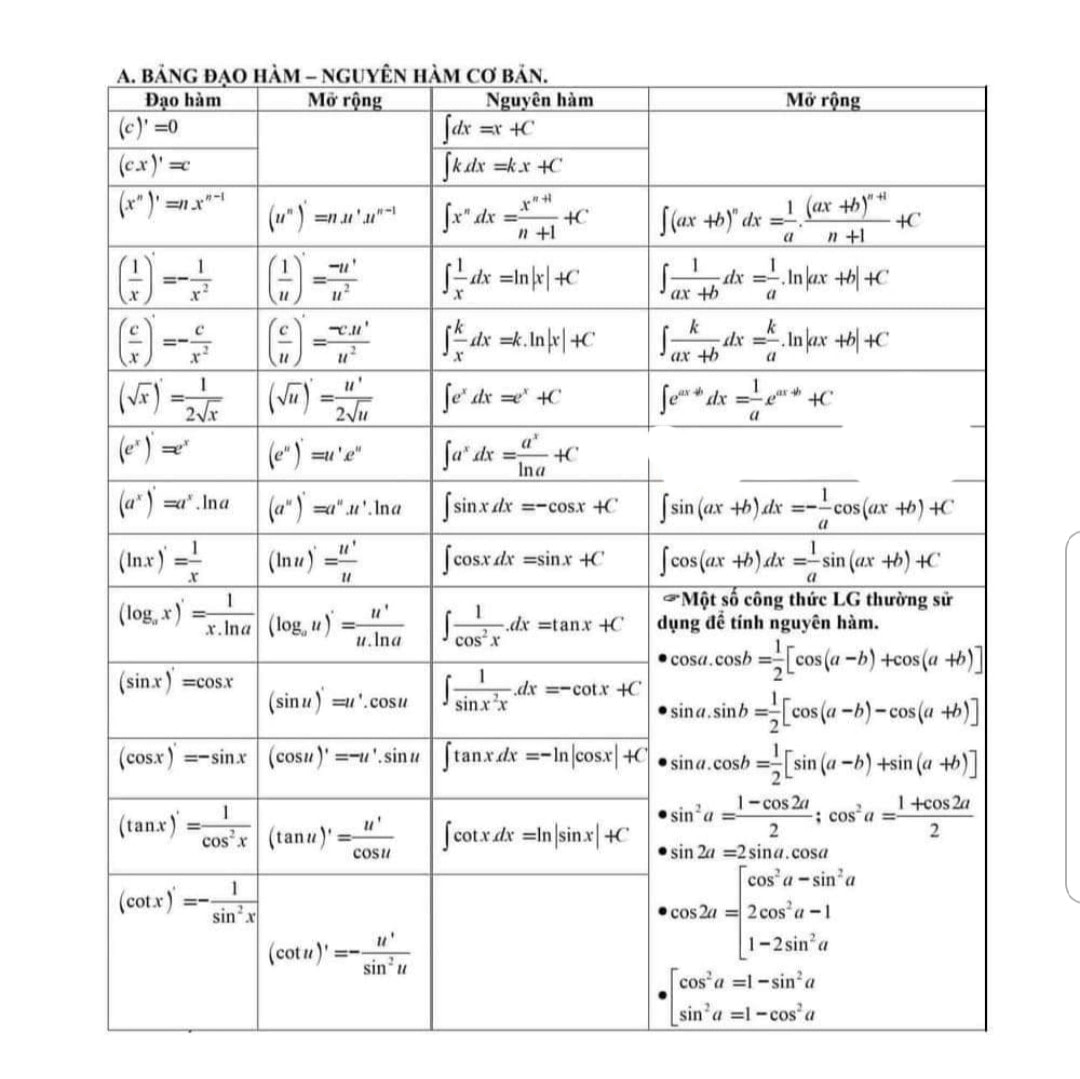
===============
====================
Thuộc chủ đề: Trắc nghiệm Nguyên hàm
Câu hỏi:
Tính \(\smallint {e^{{{\cos }^2}x}}\sin 2xdx\) bằng
Lời Giải:
Đây là các câu trắc nghiệm về NGUYÊN HÀM mức độ 1,2 
===============
====================
Thuộc chủ đề: Trắc nghiệm Nguyên hàm
