Tính (int x cdot 2^{x} d x) - Sách Toán

adsense

Câu hỏi:
Tính $\int x \cdot 2^{x} d x$

A. $\frac{x \cdot 2^{x}}{\ln 2}-\frac{2^{x}}{\ln ^{2} 2}+C$

B. $\frac{2^{x}(x-1)}{\ln 2}+C$

C. $2^{x}(x+1)+C$

D. $2^{x}(x-1)+C$

Lời Giải:
Đây là các câu trắc nghiệm về NGUYÊN HÀM mức độ 1,2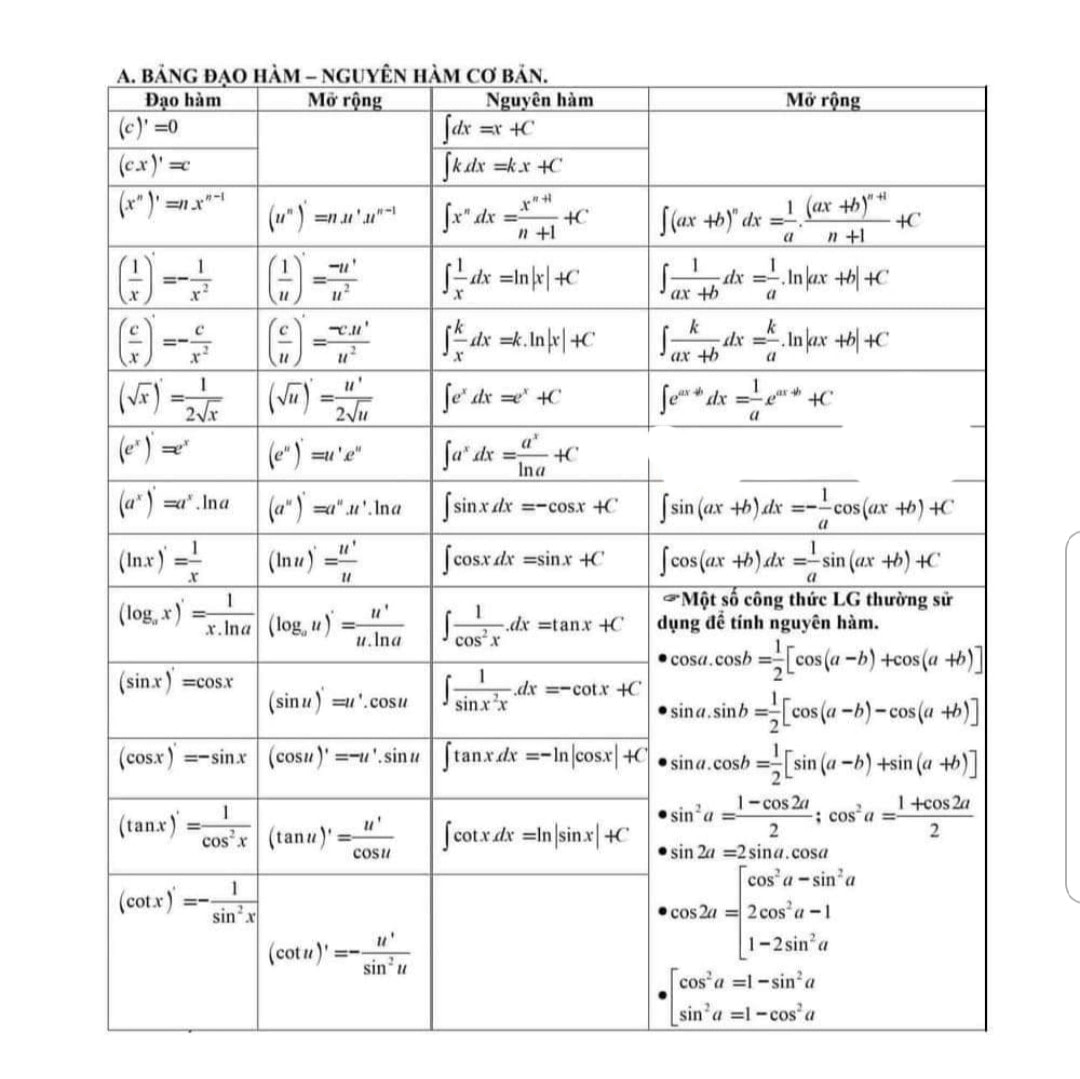
$Tính (int x cdot 2^{x} d x) 1$

Đặt $\left\{\begin{array}{l}
u=x \\
d v=2^{x} d x
\end{array} \Rightarrow\left\{\begin{array}{l}
d u=d x \\
v=\frac{2^{x}}{\ln 2}
\end{array}\right.\right.$

Khi đó

adsense

$\int x 2^{x} d x=\frac{x \cdot 2^{x}}{\ln 2}-\int \frac{2^{x}}{\ln 2} d x=\frac{x \cdot 2^{x}}{\ln 2}-\frac{2^{x}}{\ln ^{2} 2}+C$

===============

====================
Thuộc chủ đề: Trắc nghiệm Nguyên hàm

Reader Interactions

Trả lời Hủy