Tìm nguyên hàm (J = smallint frac{{x{e^x} + 1}}{{{{left( {x + {e^x}} right)}^2}}}dx) - Sách Toán

adsense

Câu hỏi:
Tìm nguyên hàm $J = \smallint \frac{{x{e^x} + 1}}{{{{\left( {x + {e^x}} \right)}^2}}}dx$

A. $\frac{{x + 1}}{{x + {e^x}+x}} + C$

B. $- \frac{{x + 1}}{{x + {e^x}+x}} + C$

C. $- \frac{{x + 1}}{{x + {e^x}}} + C$

D. $ \frac{{x + 1}}{{x + {e^x}}} +2x+ C$

Lời Giải:
Đây là các câu trắc nghiệm về NGUYÊN HÀM mức độ 1,2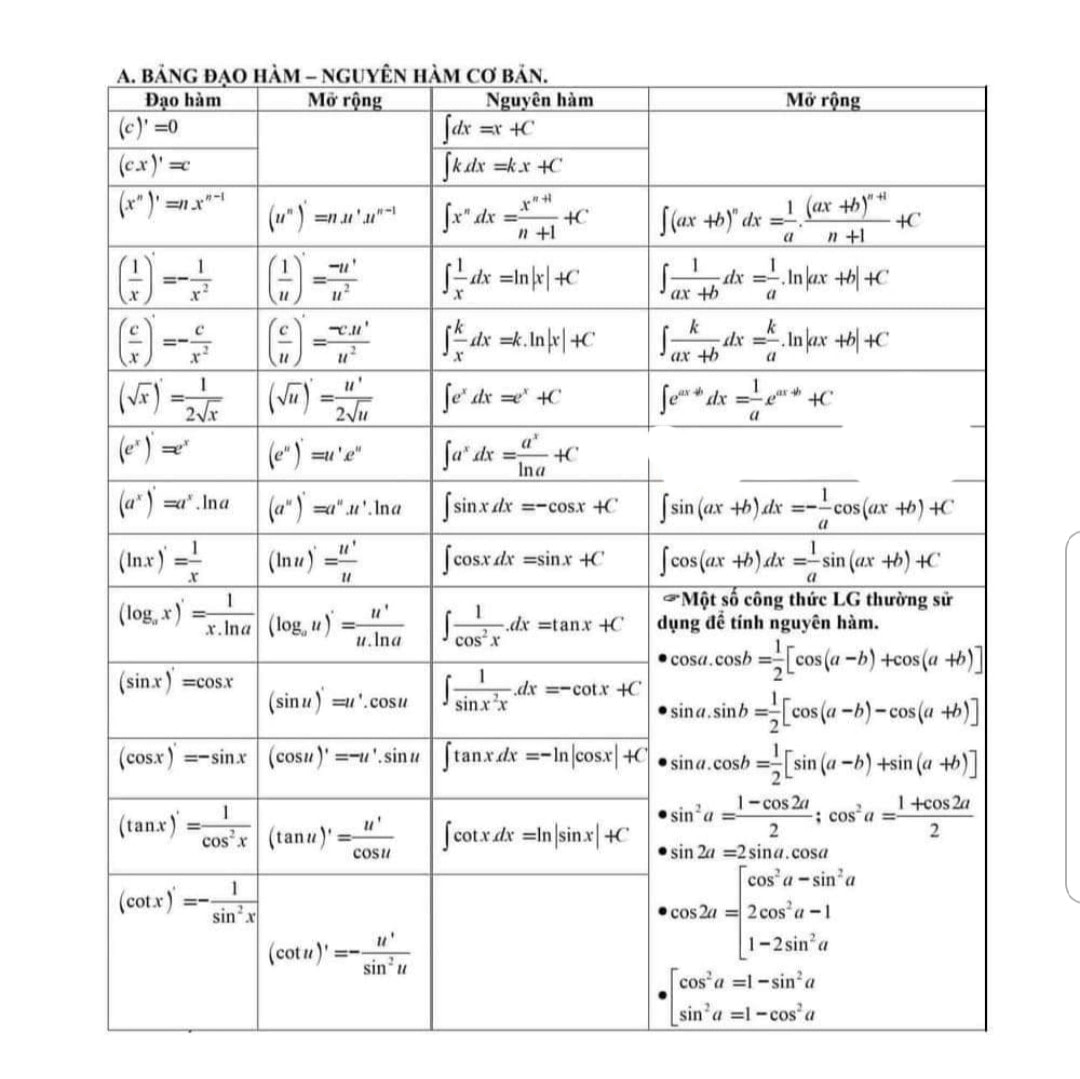
$Tìm nguyên hàm (J = smallint frac{{x{e^x} + 1}}{{{{left( {x + {e^x}} right)}^2}}}dx) 1$

$\begin{array}{l}
\frac{{x{e^x} + 1}}{{{{\left( {x + {e^x}} \right)}^2}}} = – \frac{{\left( {x + 1} \right)’\left( {x + {e^x}} \right) – \left( {x + {e^x}} \right)’\left( {x + 1} \right)}}{{{{\left( {x + {e^x}} \right)}^2}}} = – \left( {\frac{{x + 1}}{{x + {e^x}}}} \right)’\\
\Rightarrow J = – \int {\left( {\frac{{x + 1}}{{x + {e^x}}}} \right)dx = – \frac{{x + 1}}{{x + {e^x}}} + C}
\end{array}$

adsense

===============

====================
Thuộc chủ đề: Trắc nghiệm Nguyên hàm

Reader Interactions

Trả lời Hủy