GBT Chuong 4 toan 10 - KN

Giải bài tập Cuối chương 4 (Kết nối) ------------- Giải bài 4.27 trang 71 SGK Toán 10 Kết nối tri thức tập 1 Trong mặt phẳng tọa độ, cặp vectơ nào sau đây có cùng phương? A. \(\overrightarrow u  = (2;3)\) và \(\overrightarrow v  = \left( {\frac{1}{2};6} \right)\) B. \(\overrightarrow a  = (\sqrt 2 ;6)\) và \(\overrightarrow b  = (1;3\sqrt 2 … [Đọc thêm...] vềGiải bài tập Cuối chương 4 (Kết nối)

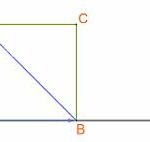
Giải bài tập Bài 11: Tích vô hướng của hai vectơ (Kết nối) =============== Giải bài 4.21 trang 70 SGK Toán 10 Kết nối tri thức tập 1 Trong mặt phẳng tọa độ Oxy, hãy tính góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) trong mỗi trường hợp sau: a) \(\overrightarrow a  = ( - 3;1),\;\overrightarrow b  = (2;6)\) b) \(\overrightarrow a  = … [Đọc thêm...] vềGiải bài tập Bài 11: Tích vô hướng của hai vectơ (Kết nối)

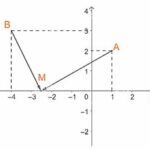
Giải bài tập Bài 10: Vectơ trong mặt phẳng tọa độ (Kết nối)   Giải bài 4.16 trang 65 SGK Toán 10 Kết nối tri thức tập 1 Trong mặt phẳng tọa độ Oxy, cho các điểm M(1; 3), N(4; 2) a) Tính độ dài các đoạn thẳng OM, ON, MN. b) Chứng minh rằng tam giác OMN vuông cân. Phương pháp giải Độ dài vectơ \(\overrightarrow … [Đọc thêm...] vềGiải bài tập Bài 10: Vectơ trong mặt phẳng tọa độ (Kết nối)

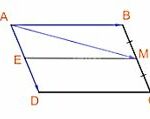
Giải bài tập Bài 9: Tích của một vectơ với một số (Kết nối) ============== Giải bài 4.11 trang 50 SGK Toán 10 Kết nối tri thức tập 1 Cho hình bình hành ABCD. Gọi M là trung điểm của cạnh BC. Hãy biểu thị \(\overrightarrow {AM} \)  theo hai vecto \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \).   Phương pháp giải Bước 1: Phân tích vecto … [Đọc thêm...] vềGiải bài tập Bài 9: Tích của một vectơ với một số (Kết nối)

Giải bài tập Bài 8: Tổng và hiệu của hai vectơ (Kết nối) ============= Giải bài 4.6 trang 54 SGK Toán 10 Kết nối tri thức tập 1 Cho bốn điểm \(A, B, C, D\). Chứng minh rằng: a)  \(\overrightarrow {AB}  + \overrightarrow {BC}  + \overrightarrow {CD}  + \overrightarrow {DA}  = \overrightarrow 0 \) b) \(\overrightarrow {AC}  - \overrightarrow {AD}  = … [Đọc thêm...] vềGiải bài tập Bài 8: Tổng và hiệu của hai vectơ (Kết nối)

Giải bài tập Bài 7: Các khái niệm mở đầu (Kết nối) ======== Giải bài 4.1 trang 50 SGK Toán 10 Kết nối tri thức tập 1 Cho 3 vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đều khác \(\overrightarrow 0 \). Những khẳng định nào sau đây là đúng? a) \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đều cùng hướng với vectơ … [Đọc thêm...] vềGiải bài tập Bài 7: Các khái niệm mở đầu (Kết nối)