Sách Toán - Học toán
Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán
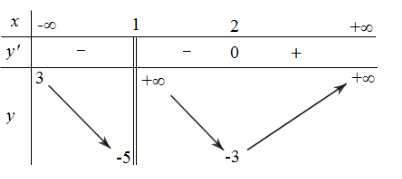
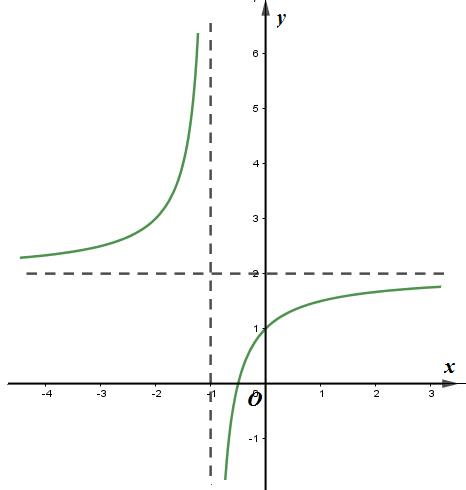
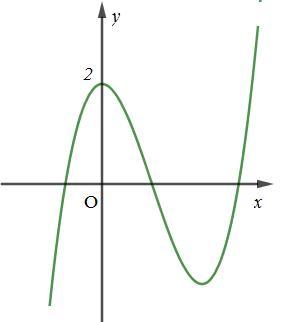
Đề thi HK1 Toán 12 năm học 2019 – 2020 – trường THPT Tân Châu Câu 1. Hình đa diện dưới đây gồm bao nhiêu mặt A. \(13\). B. \(8\). C. \(11\). D. \(9\). Câu 2. Cho \(a\) là số thực dương tùy ý, \(\dfrac{{{a^{\dfrac{2}{3}}}.{a^{\dfrac{3}{4}}}}}{{\sqrt[6]{a}}}\) bằng A. \({a^{\dfrac{1}{3}}}\). … [Đọc thêm...] vềĐề thi HK1 Toán 12 năm học 2019 – 2020 – trường THPT Tân Châu
Đề thi HK1 Toán 6 năm học 2019 – 2020 – phòng GDĐT Tân Phú ========= Bài 1 : (2,5 điểm) Thực hiện các phép tính hợp lý: \(a)\,\,16.18 + 16.32\) \(b)\,\,\left[ {243 - {{\left( {20 - 18} \right)}^3}} \right]:5\) \(c)\,\,\,\left[ {{3^{22}}.\left( {{3^8}:{3^3}} \right) + {{2.3}^{27}}} \right]:{3^{26}}\) Bài 2: (1,5 điểm) Tính giá trị của số tự … [Đọc thêm...] vềĐề thi HK1 Toán 6 năm học 2019 – 2020 – phòng GDĐT Tân Phú
Câu 41 : Hàm số \(y = - \dfrac{{{x^3}}}{3} + \left( {m - 1} \right){x^2} + \left( {m + 3} \right)x + 1\) đồng biến trên khoảng \(\left( {0;3} \right)\) khi \(m \in \left[ {\dfrac{a}{b}; + \infty } \right)\), với \(a,b \in \mathbb{Z}\) và \(\dfrac{a}{b}\) là phân số tối giản. Giá trị của biểu thức \(T = {a^2} + {b^2}\) bằng A. \(319\) B. … [Đọc thêm...] vềĐề thi HK1 Toán 12 năm học 2019 – 2020 – Bạc Liêu
Đề bài Câu 1 : Đường thẳng nào cho dưới đây là tiệm cận ngang của đồ thị hàm số \(y = \dfrac{{2x - 3}}{{x + 1}} \). A. \(y = - 2 \) . B. \(y = - 1 \) . C. \(x = 2 \) . D. \(y = 2 \). Câu 2 : Cho hàm số \(f\left( x \right) = {x^2}\ln x \). Tính \(f'\left( e \right) \). A. \(3e \) . B. \(2e \) . C. \(e \) . D. … [Đọc thêm...] vềĐề thi HK1 Toán 12 – Mẫu 5
Đề bài Câu 1 . Số mặt phẳng đối xứng của hình chóp đều \(S.ABC\) là A. \(4\) . B. \(2\) . C. \(6\) . D. \(3\) . Câu 2 . Cho \(a\) là số thực dương khác \(1\) . Hình nào sau đây là đồ thị của hàm số mũ \(y = {a^x}\)? Câu 3 . Khối cầu \((S)\) có bánh kính bằng \(r\) và thể tích bằng \(V\). Mệnh đề nào dưới đây đúng? A. \(V = … [Đọc thêm...] vềĐề thi HK1 Toán 12 – Mẫu 4
Đề bài Câu 1 : Cho hình nón đỉnh \(S\) có đường cao bằng 6 cm, bán kính đáy bằng 10 cm. Trên đường tròn đáy lấy hai điểm \(A,\,B\) sao cho \(AB = 12\)cm. Diện tích tam giác \(SAB\) bằng: A. \(100c{m^2}\). B. \(48c{m^2}\). C. \(40c{m^2}\). D. \(60c{m^2}\). Câu 2 : Cho hình chóp\(S.ABCD\) có đáy \(ABCD\) là hình bình hành và có thể tích bằng … [Đọc thêm...] vềĐề thi HK1 Toán 12 – Mẫu 3
Đề bài Câu 1 : Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? A. \(y = {x^3} - 3{x^2} + 2 \). B. \(y = {x^3} + 3{x^2} + 2 \). C. \(y = - {x^3} + 3{x^2} + 2 \). D. \(y = - {x^3} + 6{x^2} + 2 \). Câu 2 : Cho hàm số \(y = \dfrac{{ax + b}}{{x - c}} \) có đồ thị như hình vẽ … [Đọc thêm...] vềĐề thi HK1 Toán 12 – Mẫu 2
Đề bài A. PHẦN CHUNG (80%, gồm 40 câu) Câu 1 : Tìm khoảng nghịch biến của hàm số \(y = {x^3} + 3{x^2} + 2\). A. \(\left( {2; + \infty } \right)\). B. \(\left( {0;2} \right)\). C. \(\left( { - 2;0} \right)\). D. \(\left( { - \infty ;2} \right)\);\(\left( {0; + \infty } \right)\). Câu 2 : Hình đa diện đều nào dưới đây không có tâm đối … [Đọc thêm...] vềĐề thi HK1 Toán 12 – Mẫu 1
1. Công thức mũ và lũy thừa Cho a và b>0, m và n là những số thực tùy ý, ta có các công thức mũ và lũy thừa sau: 2. Công thức lôgarit Cho \(a<0\ne1,b>0\) và \(x,y>0,\) ta có các công thức sau: Công thức đổi cơ số: 3. Đạo hàm của hàm số lũy thừa, hàm số mũ và hàm số lôgarit 4. Hàm số lũy thừa, hàm số mũ, hàm số lôgarit a) Hàm số lũy thừa … [Đọc thêm...] vềHọc toán ôn tập chương 2 giải tích 12
Bất phương trình lôgarit Kiến thức cần nhớ - Tính đơn điệu của các hàm số \(y = {\log _a}x\) + Với \(0 < a < 1\) thì hàm số \(y = {\log _a}x\) nghịch biến. + Với \(a > 1\) thì hàm số \(y = {\log _a}x\) đồng biến. a) Phương pháp đưa về cùng cơ số Với \(a>1:\) \(\log_a \ f(x) >\log_a \ g(x)\)\(\Leftrightarrow \left\{\begin{matrix} f(x)>g(x)\\ … [Đọc thêm...] vềHọc toán Bài 6 Bất phương trình Logarit
