Câu hỏi:
Khi tính nguyên hàm \(\int \frac{x-3}{\sqrt{x+1}} \mathrm{~d} x\) bằng cách đặt \(u=\sqrt{x+1}\) ta được nguyên hàm nào?
Lời Giải:
Đây là các câu trắc nghiệm về NGUYÊN HÀM mức độ 1,2 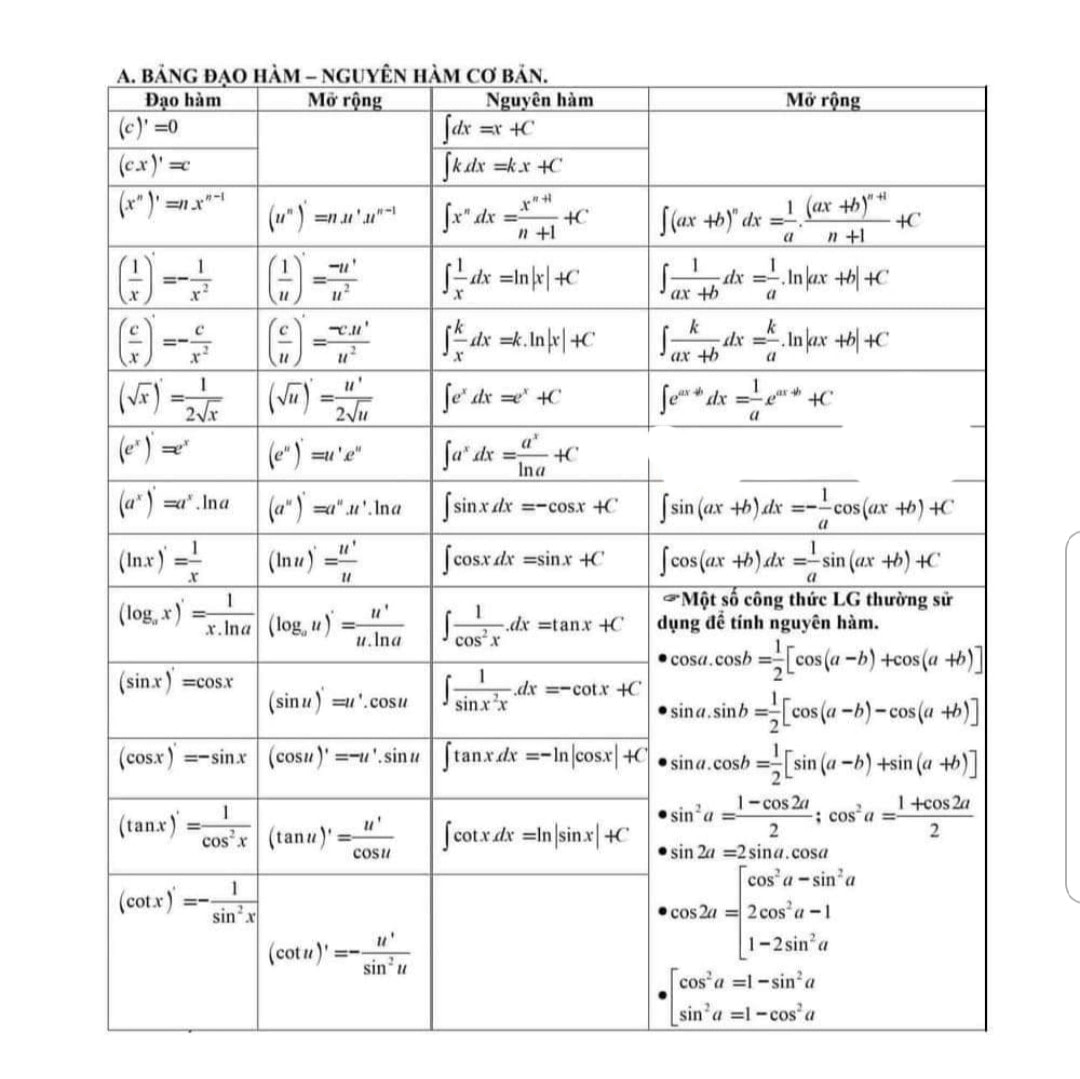
\(\begin{array}{l}
\text { Đặt } u=\sqrt{x+1}, u \geq 0 \text { nên } u^{2}=x+1 \Rightarrow\left\{\begin{array}{l}
\mathrm{d} x=2 u \mathrm{~d} u \\
x=u^{2}-1
\end{array}\right. \\
\text { Khi đó } \int \frac{x-3}{\sqrt{x+1}} \mathrm{~d} x=\int \frac{u^{2}-1-3}{u} .2 u \mathrm{~d} u=\int 2\left(u^{2}-4\right) \mathrm{d} u .
\end{array}\)
===============
====================
Thuộc chủ đề: Trắc nghiệm Nguyên hàm
