GIẢI CHI TIẾT Giải SBT Bài 5 Chương 3 – SBT Toán 10 CÁNH DIỀU
===========
Giải bài 36 trang 59 SBT Toán 10 Cánh diều tập 1 – CD
Trong các phát biểu sau, phát biểu nào là đúng?
A. Tập nghiệm của phương trình \(\sqrt {f\left( x \right)} = \sqrt {g\left( x \right)} \) là tập nghiệm của phương trình \(f\left( x \right) = g\left( x \right)\)
B. Tập nghiệm của phương trình \(\sqrt {f\left( x \right)} = \sqrt {g\left( x \right)} \) là tập nghiệm của phương trình \({\left[ {f\left( x \right)} \right]^2} = {\left[ {g\left( x \right)} \right]^2}\)
C. Tập nghiệm của phương trình \(f\left( x \right) = g\left( x \right)\) là tập nghiệm của phương trình \(\sqrt {f\left( x \right)} = \sqrt {g\left( x \right)} \)
D. Tập nghiệm của phương trình \(\sqrt {f\left( x \right)} = \sqrt {g\left( x \right)} \) là tập nghiệm của phương trình \(f\left( x \right) = g\left( x \right)\) thỏa mãn bất phương trình \(f\left( x \right) \ge 0\) (hoặc \(g\left( x \right) \ge 0\))
Phương pháp giải
\(\sqrt {f\left( x \right)} = \sqrt {g\left( x \right)} \Leftrightarrow \left\{ \begin{array}{l}f(x) \ge 0\\f\left( x \right) = g\left( x \right)\end{array} \right.\)hoặc \(\left\{ \begin{array}{l}g(x) \ge 0\\f\left( x \right) = g\left( x \right)\end{array} \right.\)
Lời giải chi tiết
Ta có: \(\sqrt {f\left( x \right)} = \sqrt {g\left( x \right)} \Leftrightarrow \left\{ \begin{array}{l}f(x) \ge 0\\f\left( x \right) = g\left( x \right)\end{array} \right.\)
Do đó tập nghiệm của phương trình \(\sqrt {f\left( x \right)} = \sqrt {g\left( x \right)} \) là tập nghiệm của phương trình \(f\left( x \right) = g\left( x \right)\) thỏa mãn bất phương trình \(f\left( x \right) \ge 0\) (hoặc \(g\left( x \right) \ge 0\))
Chọn D.
GIẢI SBT Toán 10 Cánh Diều Chương 3 Bài 5
Giải bài 37 trang 60 SBT Toán 10 Cánh diều tập 1 – CD
Trong các phát biểu sau, phát biểu nào là đúng?
A. Tập nghiệm của phương trình \(\sqrt {f\left( x \right)} = g\left( x \right)\) là tập nghiệm của phương trình \(f\left( x \right) = {\left[ {g\left( x \right)} \right]^2}\)
B. Tập nghiệm của phương trình \(\sqrt {f\left( x \right)} = g\left( x \right)\) là tập nghiệm của phương trình \(f\left( x \right) = {\left[ {g\left( x \right)} \right]^2}\) thỏa mãn bất phương trình \(g\left( x \right) \ge 0\)
C. Tập nghiệm của phương trình \(f\left( x \right) = {\left[ {g\left( x \right)} \right]^2}\) là tập nghiệm của phương trình \(\sqrt {f\left( x \right)} = g\left( x \right)\)
D. Tập nghiệm của phương trình \(\sqrt {f\left( x \right)} = g\left( x \right)\) là tập nghiệm của phương trình \(f\left( x \right) = {\left[ {g\left( x \right)} \right]^2}\) thỏa mãn bất phương trình \(f\left( x \right) \ge 0\)
Phương pháp giải
\(\sqrt {f\left( x \right)} = g\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}g\left( x \right) \ge 0\\f\left( x \right) = {\left[ {g\left( x \right)} \right]^2}\end{array} \right.\)
Lời giải chi tiết
Ta có: \(\sqrt {f\left( x \right)} = g\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}g\left( x \right) \ge 0\\f\left( x \right) = {\left[ {g\left( x \right)} \right]^2}\end{array} \right.\)
Tập nghiệm của phương trình \(\sqrt {f\left( x \right)} = g\left( x \right)\) là tập nghiệm của phương trình \(f\left( x \right) = {\left[ {g\left( x \right)} \right]^2}\) thỏa mãn bất phương trình \(g\left( x \right) \ge 0\)
Chọn B.
GIẢI SBT Toán 10 Cánh Diều Chương 3 Bài 5
Giải bài 38 trang 60 SBT Toán 10 Cánh diều tập 1 – CD
Giải thích vì sao chỉ cần kiểm tra nghiệm của phương trình \(f\left( x \right) = g\left( x \right)\) thỏa mãn một trong hai bất phương trình \(f\left( x \right) \ge 0\) hoặc \(g\left( x \right) \ge 0\) mà không cần kiểm tra thỏa mãn đồng thời hai bất phương trình đó để kết luận nghiệm của phương trình \(\sqrt {f\left( x \right)} = \sqrt {g\left( x \right)} \)
Phương pháp giải
\(\sqrt {f\left( x \right)} = \sqrt {g\left( x \right)} \Leftrightarrow \left\{ \begin{array}{l}f\left( x \right) \ge 0\\f\left( x \right) = g\left( x \right)\end{array} \right.\)
Lời giải chi tiết
Ta có \(\sqrt {f\left( x \right)} = \sqrt {g\left( x \right)} \Leftrightarrow \left\{ \begin{array}{l}f\left( x \right) \ge 0\\f\left( x \right) = g\left( x \right)\end{array} \right.\)
Khi \(f\left( x \right) \ge 0\) và \(f\left( x \right) = g\left( x \right)\) thì \(g\left( x \right) \ge 0\) và ngược lại.
Nên chỉ cần kiểm tra nghiệm của phương trình \(f\left( x \right) = g\left( x \right)\) thỏa mãn một trong hai bất phương trình \(f\left( x \right) \ge 0\) hoặc \(g\left( x \right) \ge 0\) mà không cần kiểm tra thỏa mãn đồng thời hai bất phương trình đó để kết luận nghiệm của phương trình \(\sqrt {f\left( x \right)} = \sqrt {g\left( x \right)} \)
GIẢI SBT Toán 10 Cánh Diều Chương 3 Bài 5
Giải bài 39 trang 60 SBT Toán 10 Cánh diều tập 1 – CD
Giải thích vì sao chỉ cần kiểm tra nghiệm của phương trình \(f\left( x \right) = {\left[ {g\left( x \right)} \right]^2}\) thỏa mãn bất phương trình \(g\left( x \right) \ge 0\) mà không cần kiểm tra thỏa mãn bất phương trình \(f\left( x \right) \ge 0\) để kết luận nghiệm của phương trình \(\sqrt {f\left( x \right)} = g\left( x \right)\)
Phương pháp giải
\(\sqrt {f\left( x \right)} = g\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}g\left( x \right) \ge 0\\f\left( x \right) = {\left[ {g\left( x \right)} \right]^2}\end{array} \right.\)
Lời giải chi tiết
\(\sqrt {f\left( x \right)} \ge 0 \Rightarrow g\left( x \right) \ge 0\) Khi đó \(f\left( x \right) = {\left[ {g\left( x \right)} \right]^2} \ge 0\), thỏa mãn ĐKXĐ của căn thức.
Ta có \(\sqrt {f\left( x \right)} = g\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}g\left( x \right) \ge 0\\f\left( x \right) = {\left[ {g\left( x \right)} \right]^2}\end{array} \right.\)
Nên chỉ cần kiểm tra nghiệm của phương trình \(f\left( x \right) = {\left[ {g\left( x \right)} \right]^2}\) thỏa mãn bất phương trình \(g\left( x \right) \ge 0\) mà không cần kiểm tra thỏa mãn bất phương trình \(f\left( x \right) \ge 0\) để kết luận nghiệm của phương trình \(\sqrt {f\left( x \right)} = g\left( x \right)\)
GIẢI SBT Toán 10 Cánh Diều Chương 3 Bài 5
Giải bài 40 trang 60 SBT Toán 10 Cánh diều tập 1 – CD
Giải các phương trình sau:
a) \(\sqrt { – 4x + 4} = \sqrt { – {x^2} + 1} \)
b) \(\sqrt {3{x^2} – 6x + 1} = \sqrt {{x^2} – 3} \)
c) \(\sqrt {2x – 1} = 3x – 4\)
d) \(\sqrt { – 2{x^2} + x + 7} = x – 3\)
Phương pháp giải
+ \(\sqrt {f\left( x \right)} = \sqrt {g\left( x \right)} \Leftrightarrow \left\{ \begin{array}{l}f\left( x \right) \ge 0\\f\left( x \right) = g\left( x \right)\end{array} \right.\)
+ \(\sqrt {f\left( x \right)} = g\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}g\left( x \right) \ge 0\\f\left( x \right) = {\left[ {g\left( x \right)} \right]^2}\end{array} \right.\)
Lời giải chi tiết
a) \(\sqrt { – 4x + 4} = \sqrt { – {x^2} + 1} \)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l} – 4x + 4 \ge 0\\ – 4x + 4 = – {x^2} + 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \le 1\\{x^2} – 4x + 3 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \le 1\\\left[ \begin{array}{l}x = 1\\x = 3\;(L)\end{array} \right.\end{array} \right.\quad \Leftrightarrow x = 1\end{array}\)
Vậy \(S = \left\{ 1 \right\}\)
b) \(\sqrt {3{x^2} – 6x + 1} = \sqrt {{x^2} – 3} \)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}{x^2} – 3 \ge 0\\3{x^2} – 6x + 1 = {x^2} – 3\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x^2} – 3 \ge 0\\2{x^2} – 6x + 4 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x^2} – 3 \ge 0\\\left[ \begin{array}{l}x = 1\;(L)\\x = 2\end{array} \right.\end{array} \right.\quad \Leftrightarrow x = 2\end{array}\)
Vậy \(S = \left\{ 2 \right\}\)
c) \(\sqrt {2x – 1} = 3x – 4\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}3x – 4 \ge 0\\2x – 1 = {\left( {3x – 4} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge \frac{4}{3}\\2x – 1 = 9{x^2} – 24x + 16\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge \frac{4}{3}\\9{x^2} – 26x + 17 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge \frac{4}{3}\\\left[ \begin{array}{l}x = 1\;(L)\\x = \frac{{17}}{9}\end{array} \right.\end{array} \right. \Leftrightarrow x = \frac{{17}}{9}\end{array}\)
Vậy \(S = \left\{ {\frac{{17}}{9}} \right\}\)
d) \(\sqrt { – 2{x^2} + x + 7} = x – 3\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}x – 3 \ge 0\\ – 2{x^2} + x + 7 = {\left( {x – 3} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\ – 2{x^2} + x + 7 = {x^2} – 6x + 9\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\3{x^2} – 7x + 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\\left[ \begin{array}{l}x = 2\;(L)\\x = \frac{1}{3}\;(L)\end{array} \right.\end{array} \right.\end{array}\)
Vậy \(S = \emptyset \)
GIẢI SBT Toán 10 Cánh Diều Chương 3 Bài 5
Giải bài 41 trang 60 SBT Toán 10 Cánh diều tập 1 – CD
Giải các phương trình sau:
a) \(\sqrt {7 – 2x} + x = 2\)
b) \(\sqrt { – 2{x^2} + 7x + 1} + 3x = 7\)
Phương pháp giải
Bước 1: Đưa về PT dạng \(\sqrt {f\left( x \right)} = g\left( x \right)\)
Bước 2: \(\sqrt {f\left( x \right)} = g\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}g\left( x \right) \ge 0\\f\left( x \right) = {\left[ {g\left( x \right)} \right]^2}\end{array} \right.\)
Lời giải chi tiết
a) \(\sqrt {7 – 2x} + x = 2 \Leftrightarrow \sqrt {7 – 2x} = 2 – x\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}2 – x \ge 0\\7 – 2x = {\left( {2 – x} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 2\\7 – 2x = {x^2} – 4x + 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \le 2\\{x^2} – 2x – 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 2\\\left[ \begin{array}{l}x = 3\;(L)\\x = – 1\;\end{array} \right.\end{array} \right.\end{array}\)
Vậy \(S = \left\{ { – 1} \right\}\)
b) \(\sqrt { – 2{x^2} + 7x + 1} + 3x = 7 \Leftrightarrow \sqrt { – 2{x^2} + 7x + 1} = 7 – 3x\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}7 – 3x \ge 0\\ – 2{x^2} + 7x + 1 = {\left( {7 – 3x} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le \frac{7}{3}\\ – 2{x^2} + 7x + 1 = 9{x^2} – 42x + 49\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \le \frac{7}{3}\\11{x^2} – 49x + 48 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le \frac{7}{3}\\\left[ \begin{array}{l}x = 3\;(L)\\x = \frac{{16}}{{11}}\;\end{array} \right.\quad \end{array} \right. \Leftrightarrow x = \frac{{16}}{{11}}\;\end{array}\)
Vậy \(S = \left\{ {\frac{{16}}{{11}}} \right\}\)
GIẢI SBT Toán 10 Cánh Diều Chương 3 Bài 5
Giải bài 42 trang 60 SBT Toán 10 Cánh diều tập 1 – CD
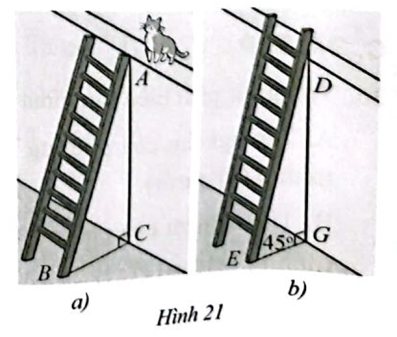
Để lao lên một bức tường, bác Dũng dùng một chiếc thang cao hơn bức tường đó 2m. Ban đầu bác Dũng đạt chiếc thang mà đầu trên của chiếc thang đó vừa chạm đúng vào mép trên của bức tường (Hình 21a). Sau đó bác Dũng dịch chuyển chân thang vào gần chân bức tường thêm 1 m thì bác Dũng thấy thang tạo với mặt đất một góc \({45^ \circ }\). Bức tường cao bao nhiêu mét?

Phương pháp giải
Lập hàm số biểu diễn chiều khoảng cách từ chân thang đến chân thường bằng chiều cao bức tường
Giải phương trình tìm chiều cao của bức tường
Lời giải chi tiết
Gọi chiều cao bức tường là \(x\) (m) (\(x > 0\)).
Suy ra chiều dài của thang là \(x + 2\) (m)
Ta có: \(AC = x,AB = x + 2\)
Khi đặt chiếc thang mà đầu trên của chiếc thang đó chạm đúng vào mép trên của bức tường thì khoảng cách chân thang đến chân tường là: \(BC = \sqrt {A{B^2} – A{C^2}} = \sqrt {{{\left( {x + 2} \right)}^2} – {x^2}} \) (m)
Khi dịch chuyển chân thang vào gần chân bức tường thêm 1m thì
\(EG = \sqrt {{{\left( {x + 2} \right)}^2} – {x^2}} – 1\)
Khi ấy thang tạo với mặt đất góc \({45^ \circ }\) nên khoảng cách từ chân thang đến chân tường bằng chiều cao bức tường hay \(EG = x\)
Ta có phương trình \(\sqrt {{{\left( {x + 2} \right)}^2} – {x^2}} – 1 = x \Leftrightarrow \sqrt {{{\left( {x + 2} \right)}^2} – {x^2}} = x + 1\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}x + 1 \ge 0\\{\left( {x + 2} \right)^2} – {x^2} = {\left( {x + 1} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge – 1\\4x + 4 = {x^2} + 2x + 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge – 1\\{x^2} – 2x – 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge – 1\\\left[ \begin{array}{l}x = – 1\;(L)\\x = 3\;\end{array} \right.\quad \end{array} \right. \Leftrightarrow x = 3\;\end{array}\)
Vậy, chiều cao của bức tường là 3 m.
GIẢI SBT Toán 10 Cánh Diều Chương 3 Bài 5
Giải bài 43 trang 61 SBT Toán 10 Cánh diều tập 1 – CD
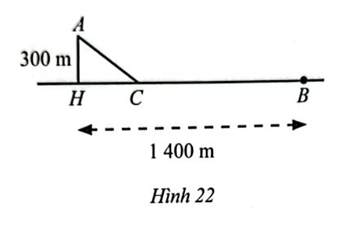
Một người đi bộ xuất phát từ B trên một bờ sông (coi là đường thẳng) với vận tốc 6 km/h để gặp một người chèo thuyền xuất phát cùng lúc từ vị trí A với vận tốc 3 km/h. Nếu người chèo thuyền di chuyển theo đường vuông góc với bờ thì phải đi một khoảng cách AH = 300 m và người đi bộ tại địa điểm cách B một khoảng BH = 1 400 m. Tuy nhiên, nếu di chuyển theo cách đó thì hai người không tới cùng lúc. Để hai người đến cùng lúc thì mỗi người cùng di chuyển về vị trí C (Hình 22).
a) Tính khoảng các CB
b) Tính thời gian từ khi hai người xuất phát cho đến khi gặp nhau cùng lúc
Phương pháp giải
Gọi \(CH = x\) (m). Biểu diễn AC và BC qua x. Giải phương trình \(\frac{{AC}}{{3.000}} = \frac{{BC}}{{6.000}}\) tìm ra CH
Lời giải chi tiết
a) Đặt \(CH = x\) (m) (\(x > 0\)). Ta có: \(AC = \sqrt {A{H^2} + C{H^2}} = \sqrt {{{300}^2} + {x^2}} ,BC = 1\;400 – CH = 1\;400 – x\)
Đổi 6 km/h = 6000 m/h; 3 km/h = 3000 m/h;
Thời gian đi đến lúc gặp nhau của người đi bộ là: \(\frac{{BC}}{{6000}} = \frac{{1400 – x}}{{6000}}\)
Thời gian đi đến lúc gặp nhau của người chèo thuyền là: \(\frac{{AC}}{{3000}} = \frac{{\sqrt {{{300}^2} + {x^2}} }}{{3000}}\)
Vì hai người gặp nhau cùng lúc tại C nên ta có: \(\frac{{\sqrt {{{300}^2} + {x^2}} }}{{3000}} = \frac{{1400 – x}}{{6000}} \Leftrightarrow 2\sqrt {{{300}^2} + {x^2}} = 1400 – x\) (với \(x > 0\))
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}x > 0\\1400 – x \ge 0\\4\left( {{{300}^2} + {x^2}} \right) = {\left( {1400 – x} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0 < x \le 1400\\4{x^2} + 360000 = {x^2} – 2800x + {1400^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}0 < x \le 1400\\3{x^2} + 2800x – 1600000 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0 < x \le 1400\\\left[ \begin{array}{l}x = – \frac{{4000}}{3}\;(L)\\x = 400\;\end{array} \right.\quad \end{array} \right. \Leftrightarrow x = 400\;\end{array}\)
Vậy khoảng cách \(BC = 1400 – 400 = 1000\) (m)
b) Thời gian từ khi hai người xuất phát cho đến khi gặp nhau là thời gian người đi bộ bắt đầu di chuyển cho đến khi gặp người chèo thuyền tại C là:
\(\frac{{BC}}{{6000}} = \frac{{1000}}{{6000}} = \frac{1}{6}\) (giờ) = 10 phút.
GIẢI SBT Toán 10 Cánh Diều Chương 3 Bài 5
Giải bài 44 trang 61 SBT Toán 10 Cánh diều tập 1 – CD
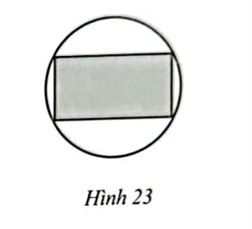
Người ta muốn thiết kế một vườn hoa hình chữ nhật nội tiếp trong một miếng đất hình tròn có đường kính bằng 50 m (Hình 23). Xác định kích thước vườn hoa hình chữ nhật để tổng quãng đường đi xung quanh vườn hoa đó là 140 m.
Phương pháp giải
Đặt độ dài 1 cạnh của hình chữ nhật là \(x\)(m) (\(0 < x < 50\)).
Biểu diễn cạnh còn lại và chu vi của hình chữ nhật theo x.
Lời giải chi tiết
Đặt độ dài một cạnh của hình chữ nhật là \(x\)(m) (\(0 < x < 50\)).
Độ dài đường chéo hình chữ nhật = Đường kính đường tròn = 50m.
Độ dài cạnh còn lại của hình chữ nhật đó là \(\sqrt {{{50}^2} – {x^2}} = \sqrt {2500 – {x^2}} \) (m)
Khi đó, tổng quãng đường đi xung quanh vườn hoa bằng chu vi hình chữ nhật là: \(2\left( {\sqrt {2500 – {x^2}} + x} \right) = 140\) (m)
Ta có phương trình: \(2\left( {\sqrt {2500 – {x^2}} + x} \right) = 140 \Leftrightarrow \sqrt {2500 – {x^2}} + x = 70 \Rightarrow \sqrt {2500 – {x^2}} = 70 – x\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}x > 0\\70 – x \ge 0\\2500 – {x^2} = {\left( {70 – x} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0 < x \le 70\\2500 – {x^2} = {x^2} – 140x + {70^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}0 < x \le 70\\2{x^2} – 140x + 2400 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0 < x \le 70\\\left[ \begin{array}{l}x = 30\\x = 40\;\end{array} \right.\quad \end{array} \right.\end{array}\)
Nếu \(x = 40\) thì độ dài cạnh còn lại là 30 (m) và ngược lại.
Vậy kích thước vườn hoa là 30 x 40 (m)
GIẢI SBT Toán 10 Cánh Diều Chương 3 Bài 5
=======
THUỘC: Giải sách bài tập toán 10 – Cánh diều
