GIẢI CHI TIẾT Giải SBT Bài 4 Chương 3 – SBT Toán 10 CÁNH DIỀU
===========
Giải bài 28 trang 56 SBT Toán 10 Cánh diều tập 1 – CD
Trong các bất phương trình sau, bất phương trình nào không là bất phương trình bậc hai một ẩn?
A. \( – 2{x^2} + 3x < 0\)
B. \(0,5{y^2} – \sqrt 3 \left( {y – 2} \right) \le 0\)
C. \({x^2} – 2xy – 3 \ge 0\)
D. \(\sqrt 2 {x^2} – 3 \ge 0\)
Phương pháp giải
Bất phương trình bậc hai một ẩn có một trong các dạng sau: \(a{x^2} + bx + c < 0;a{x^2} + bx + c > 0;a{x^2} + bx + c \le 0;a{x^2} + bx + c \ge 0\) trong đó \(a,b,c\) là các số thực và \(a \ne 0\)
Lời giải chi tiết
Bất phương trình \({x^2} – 2xy – 3 \ge 0\) có hai ẩn \(x,y\) nên nó không phải bất phương trình bậc hai một ẩn.
Chọn C.
GIẢI SBT Toán 10 Cánh Diều Chương 3 Bài 4
Giải bài 29 trang 56 SBT Toán 10 Cánh diều tập 1 – CD
Tập nghiệm của bất phương trình \( – {x^2} + 3x + 18 \ge 0\) là:
A. \(\left[ { – 3;6} \right]\)
B. \(\left( { – 3;6} \right)\)
C. \(x \in \left( { – \infty ; – 3} \right) \cup \left( {6; + \infty } \right)\)
D. \(x \in \left( { – \infty ; – 3} \right] \cup \left[ {6; + \infty } \right)\)
Phương pháp giải
Sử dụng định lý về dấu của tam thức bậc hai
Bước 1: Xác định dấu của hệ số \(a\) và tìm nghiệm của \(f\left( x \right)\) (nếu có)
Bước 2: Sử dụng định lý về dấu của tam thức bậc hai để tìm tập hợp các giá trị của của x sao cho \(f\left( x \right)\) mang dấu thỏa mãn bất phương trình
Lời giải chi tiết
Tam thức bậc hai \( – {x^2} + 3x + 18\) có hai nghiệm \({x_1} = – 3;{x_2} = 6\) và có hệ số \(a = – 1 < 0\)
Sử dụng định lý về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của \(x\) sao cho tam thức \( – {x^2} + 3x + 18 \ge 0\) mang dấu “+” là \(\left[ { – 3;6} \right]\)
Chọn A.
GIẢI SBT Toán 10 Cánh Diều Chương 3 Bài 4
Giải bài 30 trang 56 SBT Toán 10 Cánh diều tập 1 – CD
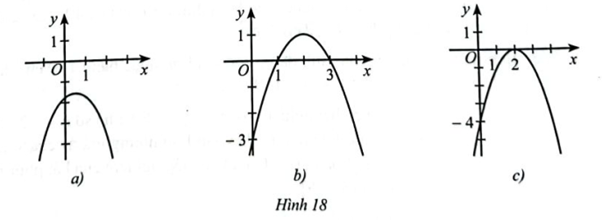
Dựa vào đồ thị hàm số bậc hai \(y = f\left( x \right)\) trong mỗi Hình 18a, 18b, 18c, hãy viết tập nghiệm các bất phương trình sau: \(f\left( x \right) > 0;f\left( x \right) < 0;f\left( x \right) \ge 0;f\left( x \right) \le 0\)

Phương pháp giải
Phần đồ thị nằm dưới trục hoành tương ứng với \(f(x) < 0\)
Phần đồ thị nằm trên trục hoành tương ứng với \(f(x) > 0\)
Dựa vào parabol \(y = a{x^2} + bx + c\), ta tìm tập hợp những giá trị của \(x\) ứng với phần trên hoặc dưới trục hoành tùy dấu của tam thức bậc hai
Lời giải chi tiết
a) Quan sát đồ thị ở Hình 18a, ta có đồ thị hàm số \(y = f(x)\) nằm phía dưới trục hoành và không cắt trục hoành nên \(f\left( x \right) < 0\) với mọi \(x \in \mathbb{R}\). Do đó:
+ Tập nghiệm của BPT \(f\left( x \right) > 0\) là \(S = \emptyset \)
+ Tập nghiệm của BPT \(f\left( x \right) < 0\) là \(S = \mathbb{R}\)
+ Tập nghiệm của BPT \(f\left( x \right) \ge 0\) là \(S = \emptyset \)
+ Tập nghiệm của BPT \(f\left( x \right) \le 0\) là \(S = \mathbb{R}\)
b) Quan sát đồ thị ở Hình 18b, ta có:
Phần đồ thị nằm trên trục hoành ứng với \(1 < x < 3\)
Phần đồ thị nằm dưới trục hoành ứng với \(x < 1\) và \(x > 3\)
Đồ thị cắt trục hoành tại điểm có hoành độ \(x = 1\) và \(x = 3\)
Kết luận
+ Tập nghiệm của BPT \(f\left( x \right) > 0\) là \(S = \left( {1;3} \right)\)
+ Tập nghiệm của BPT \(f\left( x \right) < 0\) là \(S = \left( { – \infty ;1} \right) \cup \left( {3; + \infty } \right)\)
+ Tập nghiệm của BPT \(f\left( x \right) \ge 0\) là \(S = \left[ {1;3} \right]\)
+ Tập nghiệm của BPT \(f\left( x \right) \le 0\) là \(S = \left( { – \infty ;1} \right] \cup \left[ {3; + \infty } \right)\)
c) Quan sát đồ thị ở Hình 18c, ta có đồ thị hàm số \(y = f(x)\) nằm phía dưới trục hoành và cắt trục hoành tại A(2;0) nên \(f\left( x \right) \le 0\) với mọi \(x \in \mathbb{R}\).
+ Tập nghiệm của BPT \(f\left( x \right) > 0\) là \(S = \emptyset \)
+ Tập nghiệm của BPT \(f\left( x \right) < 0\) là \(S = \mathbb{R}{\rm{\backslash }}\{ 2\} \)
+ Tập nghiệm của BPT \(f\left( x \right) \ge 0\) là \(S = 2\)
+ Tập nghiệm của BPT \(f\left( x \right) \le 0\) là \(S = \mathbb{R}\)
GIẢI SBT Toán 10 Cánh Diều Chương 3 Bài 4
Giải bài 31 trang 56 SBT Toán 10 Cánh diều tập 1 – CD
Giải các bất phương trình bậc hai sau:
a) \(3{x^2} – 8x + 5 > 0\)
b) \( – 2{x^2} – x + 3 \le 0\)
c) \(25{x^2} – 10x + 1 < 0\)
d) \( – 4{x^2} + 5x + 9 \ge 0\)
Phương pháp giải
Sử dụng định lý về dấu của tam thức bậc hai
Bước 1: Xác định dấu của hệ số \(a\) và tìm nghiệp của \(f\left( x \right)\) (nếu có)
Bước 2: Sử dụng định lý về đấu của tam thức bậc hai để tìm tập hợp các giá trị của của x sao cho \(f\left( x \right)\) mang dấu thỏa mãn bất phương trình
Lời giải chi tiết
a) \(3{x^2} – 8x + 5 > 0\)
Tam thức bậc hai \(3{x^2} – 8x + 5\) có hai nghiệm \({x_1} = 1;{x_2} = \frac{5}{3}\) và có hệ số \(a = 3 > 0\)
Sử dụng định lý về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của \(x\) sao cho tam thức \(3{x^2} – 8x + 5\) mang dấu “+” là \(\left( { – \infty ;1} \right) \cup \left( {\frac{5}{3}; + \infty } \right)\)
Vậy tập nghiệm của bất phương trình \(3{x^2} – 8x + 5 > 0\) là \(\left( { – \infty ;1} \right) \cup \left( {\frac{5}{3}; + \infty } \right)\)
b) Tam thức bậc hai \( – 2{x^2} – x + 3\) có hai nghiệm \({x_1} = – \frac{3}{2};{x_2} = 1\) và có hệ số \(a = – 2 < 0\)
Sử dụng định lý về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của \(x\) sao cho tam thức \( – 2{x^2} – x + 3\) mang dấu “-” là \(x \in \left( { – \infty ; – \frac{3}{2}} \right] \cup \left[ {1; + \infty } \right)\)
Vậy tập nghiệm của bất phương trình \( – 2{x^2} – x + 3 \le 0\) là \(x \in \left( { – \infty ; – \frac{3}{2}} \right] \cup \left[ {1; + \infty } \right)\)
c) Tam thức bậc hai \(25{x^2} – 10x + 1\) có nghiệm kép \({x_0} = \frac{1}{5}\) và có hệ số \(a = 25 > 0\)
Sử dụng định lý về dấu của tam thức bậc hai, ta thấy \(25{x^2} – 10x + 1 \ge 0\;\forall x \in \mathbb{R}\). Do đó tập hợp những giá trị của \(x\) sao cho tam thức \(25{x^2} – 10x + 1\) mang dấu “-” là \(\emptyset \)
Vậy tập nghiệm của bất phương trình \(25{x^2} – 10x + 1 < 0\) là \(\emptyset \)
d) \( – 4{x^2} + 5x + 9 \ge 0\)
Tam thức bậc hai \( – 4{x^2} + 5x + 9\) có hai nghiệm \({x_1} = – 1;{x_2} = \frac{9}{4}\) và có hệ số \(a = – 4 < 0\)
Sử dụng định lý về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của \(x\) sao cho tam thức \( – 4{x^2} + 5x + 9\) mang dấu “+” là \(\left[ { – 1;\frac{9}{4}} \right]\)
Vậy tập nghiệm của bất phương trình \( – 4{x^2} + 5x + 9 \ge 0\) là \(\left[ { – 1;\frac{9}{4}} \right]\)
GIẢI SBT Toán 10 Cánh Diều Chương 3 Bài 4
Giải bài 32 trang 57 SBT Toán 10 Cánh diều tập 1 – CD
Tìm giao các tập nghiệm của hai bất phương trình \( – 3{x^2} + 7x + 10 \ge 0\) và \( – 2{x^2} – 9x + 11 > 0\)
Phương pháp giải
Giải hai bất phương trình và kết hợp nghiệm
Lời giải chi tiết
+ Tam thức bậc hai \( – 3{x^2} + 7x + 10\) có hai nghiệm \({x_1} = – 1;{x_2} = \frac{{10}}{3}\) và có hệ số \(a = – 3 < 0\)
Sử dụng định lý về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của \(x\) sao cho tam thức \( – 3{x^2} + 7x + 10\) mang dấu “+” là \(\left[ { – 1;\frac{{10}}{3}} \right]\)
Vậy tập nghiệm của bất phương trình \( – 3{x^2} + 7x + 10 \ge 0\) là \(\left[ { – 1;\frac{{10}}{3}} \right]\)
+ Tam thức bậc hai \( – 2{x^2} – 9x + 11\) có hai nghiệm \({x_1} = – \frac{{11}}{2};{x_2} = 1\) và có hệ số \(a = – 2 < 0\)
Sử dụng định lý về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của \(x\) sao cho tam thức \( – 2{x^2} – 9x + 11\) mang dấu “+” là \(\left( { – \frac{{11}}{2};1} \right)\)
Vậy tập nghiệm của bất phương trình \( – 2{x^2} – 9x + 11 > 0\) là \(\left( { – \frac{{11}}{2};1} \right)\)
Kết hợp hai tập nghiệm \(\left[ { – 1;\frac{{10}}{3}} \right]\) và \(\left( { – \frac{{11}}{2};1} \right)\), ta có tập nghiệm của hai bất phương trình \( – 3{x^2} + 7x + 10 \ge 0\) và \( – 2{x^2} – 9x + 11 > 0\) là \(\left[ { – 1;\frac{{10}}{3}} \right] \cap \left( { – \frac{{11}}{2};1} \right) = \left[ { – 1;1} \right)\)
GIẢI SBT Toán 10 Cánh Diều Chương 3 Bài 4
Giải bài 33 trang 57 SBT Toán 10 Cánh diều tập 1 – CD
Tìm \(m\) để phương trình \( – {x^2} + \left( {m + 2} \right)x + 2m – 10 = 0\) có nghiệm
Phương pháp giải
Cho tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right),\Delta = {b^2} – 4ac\)
\(f\left( x \right) = 0\) có nghiệm \( \Leftrightarrow \Delta \ge 0\)
Lời giải chi tiết
Hàm số \( – {x^2} + \left( {m + 2} \right)x + 2m – 10 = 0\) có:
\(\begin{array}{l}a = – 1 \ne 0,b = m + 2,c = 2m – 10\\ \Rightarrow \Delta = {\left( {m + 2} \right)^2} – 4\left( { – 1} \right)\left( {2m – 10} \right)\end{array}\)
+ Phương trình \(f\left( x \right) = – {x^2} + \left( {m + 2} \right)x + 2m – 10 = 0\) có nghiệm \( \Leftrightarrow \Delta \ge 0\)
\( \Leftrightarrow {m^2} + 12m – 36 \ge 0\)
+ Giải bất phương trình \({m^2} + 12m – 36 \ge 0\)
Tam thức bậc hai \({x^2} + 12x – 36\) có hai nghiệm \({x_1} = – 6 – 6\sqrt 2 ;{x_2} = – 6 + 6\sqrt 2 \) và có hệ số \(a = 1 > 0\)
Sử dụng định lý về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của \(x\) sao cho tam thức \({x^2} + 12x – 36\) mang dấu “+” là \(\left( { – \infty ; – 6 – 6\sqrt 2 } \right] \cup \left[ { – 6 + 6\sqrt 2 ; + \infty } \right)\)
Do đó tập nghiệm của BPT \({m^2} + 12m – 36 \ge 0\) là \(\left( { – \infty ; – 6 – 6\sqrt 2 } \right] \cup \left[ { – 6 + 6\sqrt 2 ; + \infty } \right)\)
Vậy \(m \in \left( { – \infty ; – 6 – 6\sqrt 2 } \right] \cup \left[ { – 6 + 6\sqrt 2 ; + \infty } \right)\) thì phương trình trên có nghiệm
GIẢI SBT Toán 10 Cánh Diều Chương 3 Bài 4
Giải bài 34 trang 57 SBT Toán 10 Cánh diều tập 1 – CD
Xét hệ tọa độ \(Oth\) trong mặt phẳng, trong đó trục \(Ot\) biểu thị thời gian \(t\) (tính bằng giây) và trục \(Oh\) biểu thị độ cao \(h\) (tính bằng mét). Một quả bóng được đá lên từ điểm \(A\left( {0;0,3} \right)\) và chuyển động theo quỹ đạo là một cung parabol. Quả bóng đạt độ cao 8m sau 1 giây, và đạt độ cao 6m sau 2 giây. Trong khoảng thời gian nào (tính bằng giây) thì quả bóng ở độ cao lơn hơn 5m và nhỏ hơn 7m (làm tròn kết quả đến hàng phần nghìn)?
Phương pháp giải
Lập đồ thị hàm số biểu thị độ cao phụ thuộc vào thời gian
Giải bất phương trình
Lời giải chi tiết
+ Độ cao h phụ thuộc vào thời gian t theo công thức hàm số sau:
\(h\left( t \right) = – 4,85{t^2} + 12,55t + 0,3\) (m)
+ Quả bóng ở độ cao lớn hơn 5 m và hỏ hơn 7 m nên \(5 < h\left( t \right) < 7\)
+ Giải bất phương trình \( – 4,85{t^2} + 12,55t + 0,3 > 5\) hay \( – 4,85{t^2} + 12,55t – 4,7 > 0\)
Tam thức bậc hai \( – 4,85{t^2} + 12,55t – 4,7\) có hai nghiệm xấp xỉ\({t_1} = 0,454;{t_2} = 2,133\) và có hệ số \(a = – 4,85 < 0\)
Sử dụng định lý về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của \(t\) sao cho tam thức \( – 4,85{t^2} + 12,55t – 4,7\) mang dấu “+” là \(\left( {0,454;2,133} \right)\)
Do đó BPT có tập nghiệm với đầu mút xấp xỉ là \(\left( {0,454;2,133} \right)\)
+ Giải bất phương trình \( – 4,85{t^2} + 12,55t + 0,3 < 7\) hay \( – 4,85{t^2} + 12,55t – 6,7 < 0\)
Tam thức bậc hai \( – 4,85{t^2} + 12,55t – 6,7\) có hai nghiệm xấp xỉ\({t_1} = 0,735;{t_2} = 1,835\) và có hệ số \(a = – 4,85 < 0\)
Sử dụng định lý về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của \(t\) sao cho tam thức \( – 4,85{t^2} + 12,55t – 6,7\) mang dấu “-” là \(\left( { – \infty ;0,753} \right) \cup \left( {1,835; + \infty } \right)\)
Do đó BPT có tập nghiệm với đầu mút xấp xỉ là \(\left( { – \infty ;0,753} \right) \cup \left( {1,835; + \infty } \right)\)
+ Lấy giao của hai tập nghiệm trên, ta có \(t \in \left( {0,454;0,753} \right) \cup \left( {1,835;2,133} \right)\)
Vậy ở trong khoảng thời gian từ 0,454 s đến 0,753 s và từ 1,835 s đến 2,133 s thì quả bóng ở độ cao lớn hơn 5 m và nhỏ hơn 7m.
GIẢI SBT Toán 10 Cánh Diều Chương 3 Bài 4
Giải bài 35 trang 57 SBT Toán 10 Cánh diều tập 1 – CD
Một tình huống trong huấn luyện pháo binh được mô tả như sau: Trong mặt phẳng tọa độ \(Oxy\) (đơn vị trên hai trục tính theo mét), một viên đạn được bắn từ vị trí \(O\left( {0;0} \right)\) theo quỹ đạo là đường parabol \(y = – \frac{9}{{1\;000\;000}}{x^2} + \frac{3}{{100}}x\). Tìm khoảng cách theo trục hoành của viên đạn so với vị trí bắn khi viên đạn đang ở độ cao lớn hơn 15m (làm tròn kết quả đến hàng phần trăm theo đơn vị mét).
Phương pháp giải
Giải bất phương trình
Lời giải chi tiết
Độ cao viên đạn lớn hơn 15 m nên \( – \frac{9}{{1\;000\;000}}{x^2} + \frac{3}{{100}}x > 15 \Leftrightarrow – 3{x^2} + 10\;000x – 5\;000\;000 > 0\)
\( \Rightarrow \frac{{5\;000 – 1\;000\sqrt {10} }}{3} < x < \frac{{5\;000 + 1\;000\sqrt {10} }}{3}\)
Vậy khoảng cách theo trục hoành của viên đạn so với vị trí bắn viên đạn đang ở độ cao lớn hơn 15 m là nằm trong khoảng \(\left( {\frac{{5\;000 – 1\;000\sqrt {10} }}{3};\frac{{5\;000 + 1\;000\sqrt {10} }}{3}} \right)\) xấp xỉ \(\left( {612,57;2720,76} \right)\).
GIẢI SBT Toán 10 Cánh Diều Chương 3 Bài 4
=======
THUỘC: Giải sách bài tập toán 10 – Cánh diều
