GIẢI CHI TIẾT Giải SBT Bài 3 Chương 3 – SBT Toán 10 CÁNH DIỀU
===========
Giải bài 20 trang 52 SBT Toán 10 Cánh diều tập 1 – CD
Trong các phát biểu sau, phát biểu nào là sai?
A. \({x^2} – x – 2 > 0\) khi và chỉ khi \(x \in \left( { – \infty ; – 1} \right) \cup \left( {2; + \infty } \right)\)
B. \({x^2} – x – 2 \le 0\) khi và chỉ khi \(x \in \left[ { – 1;2} \right]\)
C. \({x^2} – x – 2 < 0\) khi và chỉ khi \(x \in \left( { – 1;2} \right)\)
D. \({x^2} – x – 2 \ge 0\) khi và chỉ khi \(x \in \left( { – \infty ; – 1} \right) \cup \left( {2; + \infty } \right)\)
Phương pháp giải
Xét dấu tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right),\Delta = {b^2} – 4ac\)
+ Nếu \(\Delta < 0\) thì \(f\left( x \right)\) cùng dấu với hệ số \(a\) với mọi \(x \in \mathbb{R}\)
+ Nếu \(\Delta = 0\) thì \(f\left( x \right)\) cùng dấu với hệ số \(a\) với mọi \(x \in \mathbb{R}\backslash \left\{ {\frac{{ – b}}{{2a}}} \right\}\)
+ Nếu \(\Delta > 0\) thì \(f\left( x \right)\) có hai nghiệm \({x_1},{x_2}\left( {{x_1} < {x_2}} \right)\). Khi đó:
\(f\left( x \right)\) cùng dấu với hệ số \(a\) với mọi \(x\) thuộc các khoảng \(\left( { – \infty ;{x_1}} \right) \cup \left( {{x_2}; + \infty } \right)\)
\(f\left( x \right)\) trái dấu với hệ số \(a\) với mọi \(x\) thuộc khoảng \(\left( {x{ & _1};{x_2}} \right)\)
Lời giải chi tiết
Xét hàm số \(f\left( x \right) = {x^2} – x – 2\) có \(a = 1;b = – 1,c = 2 \Rightarrow \Delta = {b^2} – 4ac = {\left( { – 1} \right)^2} – 4.1.2 = – 7\)
Đồ thị hàm số có \(a = 1 > 0\)
\( \Rightarrow {x^2} – x – 2 < 0\) khi \(x \in \left( { – 1;2} \right)\)
Và \({x^2} – x – 2 > 0\) khi \(x \in \left( { – \infty ; – 1} \right) \cup \left( {2; + \infty } \right)\)
\( \Rightarrow {x^2} – x – 2 \le 0\) khi \(x \in \left[ { – 1;2} \right]\)
Và \({x^2} – x – 2 \ge 0\) khi \(x \in ( – \infty ; – 1] \cup [2; + \infty )\)
Chọn D.
GIẢI SBT Toán 10 Cánh Diều Chương 3 Bài 3
Giải bài 21 trang 52 SBT Toán 10 Cánh diều tập 1 – CD
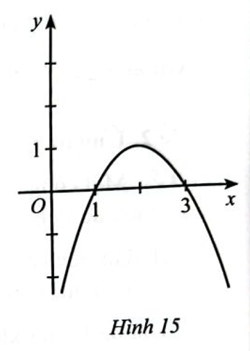
Cho hàm số \(y = f\left( x \right)\) có đồ thị ở Hình 15.

Trong các phát biểu sau, phát biểu nào là sai?
A. \(f\left( x \right) < 0\) khi và chỉ khi \(x \in \left( {1;3} \right)\)
B. \(f\left( x \right) \le 0\) khi và chỉ khi \(x \in \left( { – \infty ;1} \right] \cup \left[ {3; + \infty } \right)\)
C. \(f\left( x \right) > 0\) khi và chỉ khi \(x \in \left( {1;3} \right)\)
D. \(f\left( x \right) \ge 0\) khi và chỉ khi \(x \in \left[ {1;3} \right]\)
Phương pháp giải
Đồ thị hàm số \(f\left( x \right) < 0\) là phần đồ thị nằm dưới trục hoành và ngược lại
Lời giải chi tiết
Hình đồ thị hàm số, ta thấy
\(f\left( x \right) < 0\) khi \(x \in \left( { – \infty ;1} \right) \cup \left( {3; + \infty } \right)\)
\(f\left( x \right) = 0\) khi \(x = 1\) hoặc \(x = 3\)
\(f\left( x \right) > 0\) khi \(x \in (1;3)\)
Chọn A.
GIẢI SBT Toán 10 Cánh Diều Chương 3 Bài 3
Giải bài 22 trang 52 SBT Toán 10 Cánh diều tập 1 – CD
Cho tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\). Trong các phát biểu sau, phát biểu nào là đúng?
A. \(f\left( x \right) < 0\) với mọi \(x\) khi và chỉ khi \(a < 0\) và \(\Delta \le 0\)
B. \(f\left( x \right) < 0\) với mọi \(x\) khi và chỉ khi \(a < 0\) và \(\Delta < 0\)
C. \(f\left( x \right) \le 0\) với mọi \(x\) khi và chỉ khi \(a > 0\) và \(\Delta < 0\)
D. \(f\left( x \right) \le 0\) với mọi \(x\) khi và chỉ khi \(a > 0\) và \(\Delta \le 0\)
Phương pháp giải
Cho tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right),\Delta = {b^2} – 4ac\)
+ Nếu \(\Delta < 0\) thì \(f\left( x \right)\) cùng dấu với hệ số \(a\) với mọi \(x \in \mathbb{R}\)
+ Nếu \(\Delta = 0\) thì \(f\left( x \right)\) cùng dấu với hệ số \(a\) với mọi \(x \in \mathbb{R}\backslash \left\{ {\frac{{ – b}}{{2a}}} \right\}\)
+ Nếu \(\Delta > 0\) thì \(f\left( x \right)\) có hai nghiệm \({x_1},{x_2}\left( {{x_1} < {x_2}} \right)\). Khi đó:
\(f\left( x \right)\) cùng dấu với hệ số \(a\) với mọi \(x\) thuộc các khoảng \(\left( { – \infty ;{x_1}} \right) \cup \left( {{x_2}; + \infty } \right)\)
\(f\left( x \right)\) trái dấu với hệ số \(a\) với mọi \(x\) thuộc khoảng \(\left( {x{ & _1};{x_2}} \right)\)
Lời giải chi tiết
Ta có: \(\Delta < 0\) thì \(f\left( x \right)\) cùng dấu với hệ số \(a\) với mọi \(x \in \mathbb{R}\) nên \(f\left( x \right) < 0\) với mọi \(x\) khi và chỉ khi \(a < 0\) và \(\Delta < 0\)
Và \(f\left( x \right) \le 0\) với mọi \(x\) khi và chỉ khi \(a < 0\) và \(\Delta \le 0\)
Chọn B.
GIẢI SBT Toán 10 Cánh Diều Chương 3 Bài 3
Giải bài 23 trang 52 SBT Toán 10 Cánh diều tập 1 – CD
Lập bảng xét dấu mỗi tam thức bậc hai sau:
a) \(f\left( x \right) = 3{x^2} – 7x + 4\)
b) \(f\left( x \right) = 25{x^2} + 10x + 1\)
c) \(f\left( x \right) = 3{x^2} – 2x + 8\)
d) \(f\left( x \right) = – 2{x^2} + x + 3\)
e) \(f\left( x \right) = – 3{x^2} + 6x – 3\)
g) \(f\left( x \right) = – 5{x^2} + 2x – 4\)
Phương pháp giải
Cho tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right),\Delta = {b^2} – 4ac\)
+ Nếu \(\Delta < 0\) thì \(f\left( x \right)\) cùng dấu với hệ số \(a\) với mọi \(x \in \mathbb{R}\)
+ Nếu \(\Delta = 0\) thì \(f\left( x \right)\) cùng dấu với hệ số \(a\) với mọi \(x \in \mathbb{R}\backslash \left\{ {\frac{{ – b}}{{2a}}} \right\}\)
+ Nếu \(\Delta > 0\) thì \(f\left( x \right)\) có hai nghiệm \({x_1},{x_2}\left( {{x_1} < {x_2}} \right)\). Khi đó:

Lời giải chi tiết
a) \(f\left( x \right) = 3{x^2} – 7x + 4\) có hai nghiệm \({x_1} = 1;{x_2} = \frac{4}{3}\) và có hệ số \(a = 3 > 0\)
Ta có bảng xét dấu của \(f\left( x \right)\) như sau:
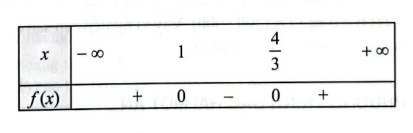
b) \(f\left( x \right) = 25{x^2} + 10x + 1\) có nghiệm kép \({x_0} = \frac{{ – 1}}{5}\) và có hệ số \(a = 25 > 0\)
Ta có bảng xét dấu của \(f\left( x \right)\) như sau:
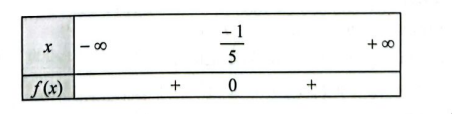
c) \(f\left( x \right) = 3{x^2} – 2x + 8\) vô nghiệm và có hệ số \(a = 3 > 0\)
Ta có bảng xét dấu của \(f\left( x \right)\) như sau:
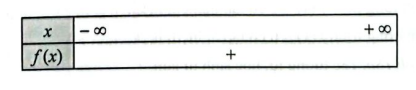
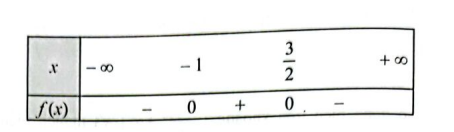
d) \(f\left( x \right) = – 2{x^2} + x + 3\) có hai nghiệm \({x_1} = – 1;{x_2} = \frac{3}{2}\) và có hệ số \(a = – 2 < 0\)
Ta có bảng xét dấu của \(f\left( x \right)\) như sau:
e) \(f\left( x \right) = – 3{x^2} + 6x – 3\) có nghiệm kép \({x_0} = 1\) và có hệ số \(a = – 3 < 0\)
Ta có bảng xét dấu của \(f\left( x \right)\) như sau:

g) \(f\left( x \right) = – 5{x^2} + 2x – 4\) vô nghiệm và có hệ số \(a = – 5 < 0\)
Ta có bảng xét dấu của \(f\left( x \right)\) như sau:

GIẢI SBT Toán 10 Cánh Diều Chương 3 Bài 3
Giải bài 24 trang 52 SBT Toán 10 Cánh diều tập 1 – CD
Tìm \(m\) để tam thức \(f\left( x \right) = – {x^2} – 2x + m – 12\) không dương với mọi \(x \in \mathbb{R}\)
Phương pháp giải
Tam thức \(f\left( x \right) = a{x^2} + bx + c \le 0\;\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}a < 0\\\Delta \le 0\end{array} \right.\)
Lời giải chi tiết
Hàm số \(f\left( x \right) = – {x^2} – 2x + m – 12 \le 0\;\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}a < 0\\\Delta \le 0\end{array} \right.\) (*)
Mà \(a = – 1 < 0\) nên
\(\left( * \right) \Leftrightarrow \Delta = {\left( { – 2} \right)^2} – 4.\left( { – 1} \right).\left( {m – 12} \right) \le 0 \Leftrightarrow 4m – 44 \le 0 \Leftrightarrow m \le 11\)
Vậy \(m \le 11\) thì tam thức đó không dương với mọi \(x \in \mathbb{R}\).
GIẢI SBT Toán 10 Cánh Diều Chương 3 Bài 3
Giải bài 25 trang 52 SBT Toán 10 Cánh diều tập 1 – CD
Với giá trị nào của tham số \(m\) thì hàm số \(y = \sqrt {2{x^2} – 5x + 3m – 2} \) có tập xác định là \(\mathbb{R}\)?
Phương pháp giải
\(\sqrt {f(x)} \) xác định khi \(f(x) \ge 0\)
Tam thức \(f\left( x \right) = a{x^2} + bx + c \ge 0\;\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta \le 0\end{array} \right.\)
Lời giải chi tiết
Hàm số \(y = \sqrt {2{x^2} – 5x + 3m – 2} \) xác định khi \(2{x^2} – 5x + 3m – 2 \ge 0\)
Do đó, hàm số có tập xác định là \(\mathbb{R}\)\( \Leftrightarrow 2{x^2} – 5x + 3m – 2 \ge 0\;\forall x \in \mathbb{R}\)
\( \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta \le 0\end{array} \right.\) (*)
Mà \(a = 2 > 0,\Delta = {\left( { – 5} \right)^2} – 4.2.\left( {3m – 2} \right) = – 24m + 41\)
Do đó \((*) \Leftrightarrow – 24m + 41 \le 0 \Leftrightarrow m \ge \frac{{41}}{{24}}\)
Vậy \(m \ge \frac{{41}}{{24}}\)
GIẢI SBT Toán 10 Cánh Diều Chương 3 Bài 3
Giải bài 26 trang 52 SBT Toán 10 Cánh diều tập 1 – CD
Tìm tất cả giá trị của \(m\) để hàm số \(y = \frac{1}{{\sqrt {{x^2} – 4x + 6m – 1} }}\) có tập xác định là \(\mathbb{R}\).
Phương pháp giải
\(\frac{1}{{\sqrt {f(x)} }}\) xác định khi \(f(x) > 0\)
Tam thức \(f\left( x \right) = a{x^2} + bx + c > 0\;\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta < 0\end{array} \right.\)
Lời giải chi tiết
Hàm số \(y = \frac{1}{{\sqrt {{x^2} – 4x + 6m – 1} }}\) xác định khi \({x^2} – 4x + 6m – 1 > 0\)
Do đó, hàm số có tập xác định là \(\mathbb{R}\)\( \Leftrightarrow {x^2} – 4x + 6m – 1 > 0\)\(\forall x \in \mathbb{R}\)
\( \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta < 0\end{array} \right.\) (*)
Mà \(a = 1 > 0,\Delta = {\left( { – 4} \right)^2} – 4.1.\left( {6m – 1} \right) = – 24m + 20\)
Do đó \((*) \Leftrightarrow – 24m + 20 < 0 \Leftrightarrow m > \frac{5}{6}\)
Vậy \(m > \frac{5}{6}\)
GIẢI SBT Toán 10 Cánh Diều Chương 3 Bài 3
Giải bài 27 trang 52 SBT Toán 10 Cánh diều tập 1 – CD
Bộ phận nghiên cứu thị trường của một xí nghiệp xác định tổng chi phí để sản xuất \(Q\) sản phẩm là \({Q^2} + 200Q + 180.000\) (nghìn đồng). Giả sử giá mỗi sản phẩm bán ra thị trường là 1 300 nghìn đồng
a) Xác định lợi nhuận xí nghiệp thu được sau khi bán hết \(Q\) sản phẩm đó, biết rằng lợi nhuận là hiệu doanh thu trừ đi tổng chi phí để sản xuất
b) Xí nghiệp cần sản xuất bao nhiêu sản phẩm để không bị lỗ? Biết rằng các sản phẩm được sản xuất ra đều bán hết
Phương pháp giải
Xác định hàm doanh thu, từ đó xác định lợi nhuận DN thu được
Doanh nghiêp không bị lỗ khi Lợi nhuận không âm, từ đó giải hệ bất phương trình
Lời giải chi tiết
a) Doanh thu của xí nghiệp là: \(DT = 1\;300Q\) (nghìn đồng)
Tổng chi phí để sản xuất \(Q\) sản phẩm là \(CP = {Q^2} + 200Q + 180\;000\) (nghìn đồng)
\( \Rightarrow \) Lợi nhuận của xí nghiệp là: \(f\left( Q \right) = DT – CP = 1300Q – \left( {{Q^2} + 200Q + 180000} \right) = – {Q^2} + 1100Q – 180000\) (nghìn đồng)
b) Xí nghiệp không bị lỗ khi và chỉ khi \(f\left( Q \right) \ge 0\)
\(f\left( x \right) = – {x^2} + 1\;100x – 180\;000\)có hai nghiệm \({x_1} = 200;{x_2} = 900\) và có hệ số \(a = – 1 < 0\)
Ta có bảng xét dấu của \(f\left( x \right)\) như sau:

Theo đó, \(f\left( Q \right) \ge 0 \Leftrightarrow Q \in \left[ {200;900} \right]\).
Vậy ví nghiệp cần sản xuất số sản phẩm trong đoạn \(\left[ {200;900} \right]\) để không bị lỗ
GIẢI SBT Toán 10 Cánh Diều Chương 3 Bài 3
=======
THUỘC: Giải sách bài tập toán 10 – Cánh diều
