GIẢI CHI TIẾT Giải SBT Bài 3 Chương 6 – SBT Toán 10 CÁNH DIỀU
===========
Giải bài 14 trang 37 SBT Toán 10 Cánh diều tập 2 – CD
Cho mẫu số liệu: 21 22 23 24 25
a) Khoảng biến thiên của mẫu số liệu trên là:
A. 1 B. 2 C. 3 D. 4
b) Khoảng tứ phân vị của mẫu số liệu trên là:
A. 1 B. 2 C. 3 D. 4
c) Phương sai của mẫu số liệu trên là:
A. 1 B. 2 C. 3 D. 4
d) Độ lệch chuẩn của mẫu số liệu trên là:
A. 1 B. \(\sqrt 2 \) C. \(\sqrt 3 \) D. 4
Phương pháp giải
+ Sắp xếp số liệu theo thứ tự không giảm và tìm khoảng biến thiên theo công thức\(R = {x_n} – {x_1}\) với số cao nhất và thấp nhất lần lượt \({x_n},{x_1}\)
+ Khoảng tứ phân vị: \(\Delta Q = {Q_3} – {Q_1}\)
Bước 1: Sắp xếp các số liệu theo thứ tự không giảm.
Bước 2: Tính cỡ mẫu \(n\), tìm tứ phân vị thứ hai \({Q_2}\)(chính là trung vị của mẫu).
Bước 3: Tìm tứ phân vị thứ nhất: là trung vị của nửa số liệu đã sắp xếp bên trái \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
Bước 4: Tìm tứ phân vị thứ ba: là trung vị của nửa số liệu đã sắp xếp bên phải \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
+ Tìm phương sai theo công thức \({S^2} = \frac{1}{n}\left( {{n_1}{x_1}^2 + {n_2}{x_2}^2 + … + {n_k}{x_k}^2} \right) – {\overline x ^2}\) và độ lệch chuẩn \(S = \sqrt {{S^2}} \)
Lời giải chi tiết
Cho mẫu số liệu: 21 22 23 24 25
a) Số cao nhất và thấp nhất lần lượt là 25 và 21 do đó khoảng biến thiên của dãy số liệu trên là: \(R = 25 – 21 = 4\)
Chọn D.
b) Tứ phân vị: \({Q_2} = 23\); \({Q_1} = \left( {21 + 22} \right):2 = 21,5;{Q_3} = \left( {24 + 25} \right):2 = 24,5 \Rightarrow \Delta Q = {Q_3} – {Q_1} = 24,5 – 21,5 = 3\)
Chọn C.
c) Phương sai: \({S^2} = 2\)
Chọn B.
d) Độ lệch chuẩn: \(S = \sqrt {{S^2}} = \sqrt 2 \)
Chọn B.
GIẢI SBT Toán 10 Cánh Diều Chương 6 Bài 3
Giải bài 15 trang 38 SBT Toán 10 Cánh diều tập 2 – CD
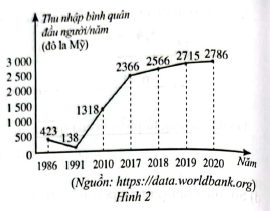
Biểu đồ đoạn thẳng ở Hình 2 biểu diễn thu nhập bình quân đầu người/ năm của VN ở một số năm trong giai đoạn từ 1986 đến 2020.

Mẫu số liệu nhận được từ biểu đồ ở HÌnh 2 có khoảng biến thiên là bao nhiêu?
A. 71 B. 85 C. 1 180 D. 2 648
Phương pháp giải
Sắp xếp số liệu theo thứ tự không giảm và tìm khoảng biến thiên theo công thức\(R = {x_n} – {x_1}\) với số cao nhất và thấp nhất lần lượt \({x_n},{x_1}\)
Lời giải chi tiết
Số cao nhất và thấp nhất lần lượt là 2786 và 138 do đó khoảng biến thiên của dãy số liệu trên là: \(R = 2786 – 138 = 2648\)
Chọn D.
GIẢI SBT Toán 10 Cánh Diều Chương 6 Bài 3
Giải bài 16 trang 38 SBT Toán 10 Cánh diều tập 2 – CD
Biểu đồ đoạn thẳng ở Hình 3 biểu diễn số lượt khách vào một cửa hàng trong ngày đầu khai trương tại một số mốc thời gian.
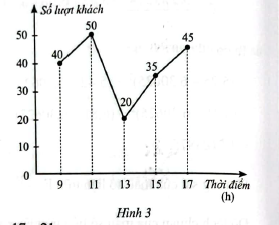
Mẫu số liệu nhận được từ biểu đồ ở Hình 3 có khoảng tứ phân vị là bao nhiêu?
A. 10 B. 15 C. 20 D. 5
Phương pháp giải
+ Khoảng tứ phân vị: \(\Delta Q = {Q_3} – {Q_1}\)
Bước 1: Sắp xếp các số liệu theo thứ tự không giảm.
Bước 2: Tính cỡ mẫu \(n\), tìm tứ phân vị thứ hai \({Q_2}\)(chính là trung vị của mẫu).
Bước 3: Tìm tứ phân vị thứ nhất: là trung vị của nửa số liệu đã sắp xếp bên trái \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
Bước 4: Tìm tứ phân vị thứ ba: là trung vị của nửa số liệu đã sắp xếp bên phải \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
Lời giải chi tiết
+ Sắp xếp mẫu số liệu theo thứ tự không giảm ta được: \(20;35;40;45;50\)
+ Vì \(n = 5\) là số lẻ nên tứ phân vị thứ hai là: \({Q_2} = 40\) là tứ phân vị
+ Tứ phân vị thứ nhất là trung vị của 2 số đầu tiên của mẫu số liệu: \({Q_1} = \left( {20 + 35} \right):2 = 27,5\)
+ Tứ phân vị thứ ba là trung vị của 2 số cuối của mẫu số liệu: \({Q_3} = \left( {45 + 50} \right):2 = 47,5\)
+ Khoảng tứ phân vị: \(\Delta Q = {Q_3} – {Q_1} = 47,5 – 27,5 = 20\)
Chọn C.
GIẢI SBT Toán 10 Cánh Diều Chương 6 Bài 3
Giải bài 17 trang 38 SBT Toán 10 Cánh diều tập 2 – CD
Cho mẫu số liệu: 1 11 13 15 17 21
a) Tìm khoảng biến thiên của mẫu số liệu trên
b) Tìm khoảng tứ phân vị của mẫu số liệu trên
c) Tìm phương sai và độ lệch chuẩn của mẫu số liệu trên
d) Tìm giá trị bất thường của mẫu số liệu trên.
Phương pháp giải
+ Sắp xếp số liệu theo thứ tự không giảm và tìm khoảng biến thiên theo công thức\(R = {x_n} – {x_1}\) với số cao nhất và thấp nhất lần lượt \({x_n},{x_1}\)
+ Khoảng tứ phân vị: \(\Delta Q = {Q_3} – {Q_1}\)
Bước 1: Sắp xếp các số liệu theo thứ tự không giảm.
Bước 2: Tính cỡ mẫu \(n\), tìm tứ phân vị thứ hai \({Q_2}\)(chính là trung vị của mẫu).
Bước 3: Tìm tứ phân vị thứ nhất: là trung vị của nửa số liệu đã sắp xếp bên trái \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
Bước 4: Tìm tứ phân vị thứ ba: là trung vị của nửa số liệu đã sắp xếp bên phải \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
+ Tìm phương sai theo công thức \({S^2} = \frac{1}{n}\left( {{n_1}{x_1}^2 + {n_2}{x_2}^2 + … + {n_k}{x_k}^2} \right) – {\overline x ^2}\) và độ lệch chuẩn \(S = \sqrt {{S^2}} \)
+ Giá trị ngoại lệ là giá trị trong mẫu thỏa mãn \(a < {Q_1} – 1,5.{\Delta _Q}\) và \(a > {Q_3} + 1,5.{\Delta _Q}\)
Lời giải chi tiết
Cho mẫu số liệu: 1 11 13 15 17 21
a) Số cao nhất và thấp nhất lần lượt là 21 và 1 do đó khoảng biến thiên của dãy số liệu trên là: \(R = 21 – 1 = 20\)
b)
+ Vì \(n = 6\) là số chẵn nên tứ phân vị thứ hai là: \({Q_2} = \left( {13 + 15} \right):2 = 14\) là tứ phân vị
+ Tứ phân vị thứ nhất là trung vị của 3 số đầu tiên của mẫu số liệu: \({Q_1} = 11\)
+ Tứ phân vị thứ ba là trung vị của 3 số cuối của mẫu số liệu: \({Q_3} = 17\)
+ Khoảng tứ phân vị: \(\Delta Q = {Q_3} – {Q_1} = 17 – 11 = 6\)
c)
+ Số trun bình cộng: \(\overline x = \frac{{1 + 11 + 13 + 15 + 17 + 21}}{6} = 13\)
+ Phương sai: \({S^2} = \frac{1}{6}\left( {{1^2} + {{11}^2} + … + {{21}^2}} \right) – {13^2} = \frac{{116}}{3}\)
+ Độ lệch chuẩn: \(S = \sqrt {{S^2}} = \sqrt {\frac{{116}}{3}} = \frac{{2\sqrt {87} }}{3}\)
d) Ta có \({Q_1} – 1,5.{\Delta _Q} = 11 – 1,5.6 = 2\) và \({Q_3} + 1,5.{\Delta _Q} = 17 + 1,5.6 = 26\) nên mẫu có một giá trị ngoại lệ là 1.
GIẢI SBT Toán 10 Cánh Diều Chương 6 Bài 3
Giải bài 18 trang 38 SBT Toán 10 Cánh diều tập 2 – CD
Kết quả dự báo nhiệt độ cao nhất trong 10 ngày liên tiếp ở Nghệ An cuối tháng 01 năm 2022 được cho ở bảng sau:
|
Ngày |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
|
Nhiệt độ (độ C) |
23 |
25 |
26 |
27 |
27 |
27 |
27 |
21 |
19 |
18 |
a) Viết mẫu số liệu thống kê nhiệt độ nhận được từ bảng trên
b) Tính số trung bình cộng, phương sai và độ lệch chuẩn của mẫu số liệu đó
Phương pháp giải
+ Viết mẫu số liệu theo thứ tự không tăng
+ Dùng công thức tính số trung bình: \(\overline x = \frac{{{x_1} + {x_2} + … + {x_n}}}{n}\)
+ Tìm phương sai theo công thức \({S^2} = \frac{1}{n}\left( {{n_1}{x_1}^2 + {n_2}{x_2}^2 + … + {n_k}{x_k}^2} \right) – {\overline x ^2}\) và độ lệch chuẩn \(S = \sqrt {{S^2}} \)
Lời giải chi tiết
a) Viết mẫu số liệu theo thứ tự không tăng: 23; 25; 26; 27; 27; 27; 26; 21; 19; 18
b)
+ Số trung bình của mẫu số liệu là: \(\overline x = \frac{{23 + 25 + 26 + 27 + 27 + 27 + 26 + 21 + 19 + 18}}{{10}} = 24\)
+ Phương sai: \({S^2} = \frac{1}{{10}}\left( {{{23}^2} + {{25}^2} + … + {{18}^2}} \right) – {24^2} = 11,2\)
+ Độ lệch chuẩn: \(S = \sqrt {{S^2}} = \sqrt {11,2} = \frac{{2\sqrt {70} }}{5}\)
GIẢI SBT Toán 10 Cánh Diều Chương 6 Bài 3
Giải bài 19 trang 39 SBT Toán 10 Cánh diều tập 2 – CD
Biểu đồ đoạn thẳng ở Hình 4 cho biết kết quả thi Ngoại ngữ ở CLB của Dũng (đường nét liền) và Hoàng (đường nét đứt đậm) qua 9 lần kiểm tra
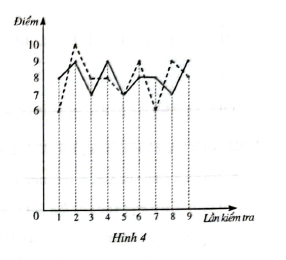
a) Viết mẫu số liệu thống kê kết quả thi ngoại ngữ của Dũng và Hoàng nhận được từ biểu đồ ở Hình 4
b) Tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu đó
c) Tính phương sai và độ lệch chuẩn của hai mẫu số liệu đó. Cho biết kết quả thi của bạn nào ổn định hơn?
Phương pháp giải
+ Liệt kê các giá trị trong biểu đồ và sắp xếp các số liệu theo thứ tự không giảm
+ Tìm khoảng biến thiên theo công thức\(R = {x_n} – {x_1}\) với số cao nhất và thấp nhất lần lượt \({x_n},{x_1}\)
+ Khoảng tứ phân vị: \(\Delta Q = {Q_3} – {Q_1}\)
Bước 1: Sắp xếp các số liệu theo thứ tự không giảm.
Bước 2: Tính cỡ mẫu \(n\), tìm tứ phân vị thứ hai \({Q_2}\)(chính là trung vị của mẫu).
Bước 3: Tìm tứ phân vị thứ nhất: là trung vị của nửa số liệu đã sắp xếp bên trái \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
Bước 4: Tìm tứ phân vị thứ ba: là trung vị của nửa số liệu đã sắp xếp bên phải \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
+ Tìm phương sai theo công thức \({S^2} = \frac{1}{n}\left( {{n_1}{x_1}^2 + {n_2}{x_2}^2 + … + {n_k}{x_k}^2} \right) – {\overline x ^2}\) và độ lệch chuẩn \(S = \sqrt {{S^2}} \)
Lời giải chi tiết
a)
+ Mẫu số liệu kết quả thi của bạn Dũng là: 8; 9; 7; 9; 7; 8; 8; 7; 9.
+ Mẫu số liệu kết quả thi của bạn Hoàng là: 6; 10; 8; 8; 7; 9; 6; 9; 8.
b)
– Sắp xếp mẫu số liệu theo thứ tự tăng dần
Mẫu số liệu kết quả thi của bạn Dũng là: 7; 7; 7; 8; 8; 8; 9; 9; 9 (1)
Mẫu số liệu kết quả thi của bạn Hoàng là: 6; 6; 7; 8; 8; 8; 9; 9; 10 (2)
– Khoảng biến thiên:
+ Mẫu số liệu (1): Số cao nhất và thấp nhất lần lượt là 9 và 7 do đó khoảng biến thiên của dãy số liệu là: \(R = 9 – 7 = 2\)
+ Mẫu số liệu (2): Số cao nhất và thấp nhất lần lượt là 10 và 6 do đó khoảng biến thiên của dãy số liệu là: \(R = 10 – 6 = 4\)
– Mẫu số liệu (1):
+ Vì \(n = 9\) là số lẻ nên tứ phân vị thứ hai là: \({Q_2} = 8\) là tứ phân vị
+ Tứ phân vị thứ nhất là trung vị của 4 số đầu tiên của mẫu số liệu: \({Q_1} = \left( {7 + 7} \right):2 = 7\)
+ Tứ phân vị thứ ba là trung vị của 4 số cuối của mẫu số liệu: \({Q_3} = \left( {9 + 9} \right):2 = 9\)
+ Khoảng tứ phân vị: \(\Delta Q = {Q_3} – {Q_1} = 9 – 7 = 2\)
– Mẫu số liệu (2):
+ Vì \(n = 9\) là số lẻ nên tứ phân vị thứ hai là: \({Q_2} = 8\) là tứ phân vị
+ Tứ phân vị thứ nhất là trung vị của 4 số đầu tiên của mẫu số liệu: \({Q_1} = \left( {6 + 7} \right):2 = 6,5\)
+ Tứ phân vị thứ ba là trung vị của 4 số cuối của mẫu số liệu: \({Q_3} = \left( {9 + 9} \right):2 = 9\)
+ Khoảng tứ phân vị: \(\Delta Q = {Q_3} – {Q_1} = 9 – 6,5 = 2,5\)
c)
– Mẫu số liệu (1):
+ Số trung bình cộng: \(\overline x = \frac{{3.7 + 3.8 + 3.9}}{9} = 8\)
+ Phương sai: \({S^2} = \frac{1}{9}({3.7^2} + {3.8^2} + {3.9^2}) – {8^2} = \frac{2}{3}\)
+ Độ lệch chuẩn: \(S = \sqrt {{S^2}} = \sqrt {\frac{2}{3}} = \frac{{\sqrt 6 }}{3}\)
– Mẫu số liệu (2):
+ Số trung bình cộng: \(\overline x = \frac{{2.6 + 7 + 3.8 + 2.9 + 10}}{9} = \frac{{71}}{9}\)
+ Phương sai: \({S^2} = \frac{1}{9}({2.6^2} + {7^2} + {3.8^2} + {2.9^2} + {10^2}) – {\left( {\frac{{71}}{9}} \right)^2} = \frac{{134}}{{81}}\)
+ Độ lệch chuẩn: \(S = \sqrt {{S^2}} = \sqrt {\frac{{134}}{{81}}} = \frac{{\sqrt {134} }}{9}\)
Ta có: \(\frac{2}{3} < \frac{{134}}{{81}}\) nên kết quả thi của bạn Dũng ổn định hơn
GIẢI SBT Toán 10 Cánh Diều Chương 6 Bài 3
=======
THUỘC: Giải sách bài tập toán 10 – Cánh diều
