Giải SBT bài 1: Tập hợp Q các số hữu tỉ (C1 SBT Toán 7 Cánh diều)

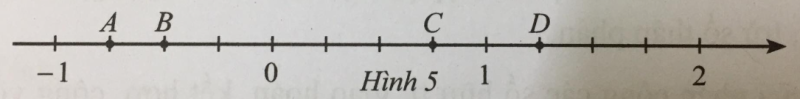
Giải bài 1 trang 9 SBT Toán 7 Cánh diều tập 1

Phương pháp giải:

Số hữu tỉ là số viết được dưới dạng phân số \(\dfrac{a}{b}\) với \(a,{\rm{ }}b \in \mathbb{Z},{\rm{ }}b \ne 0\).

Mỗi số nguyên là một số hữu tỉ. 

Lời giải chi tiết:

Các số \(0,5; 11; 3,111; 4\dfrac{5}{7}; – 34; – 1,3; \dfrac{{ – 1}}{{ – 3}}; \dfrac{{ – 9}}{8}\) có là số hữu tỉ.

Vì ngoài \(\dfrac{{ – 1}}{{ – 3}}\); \(\dfrac{{ – 9}}{8}\) đã được viết dưới dạng phân số thì những số còn lại cũng viết được dưới dạng phân số. Cụ thể:

\(0,5{\rm{  = }}\dfrac{5}{{10}};{\rm{ }}11 = \dfrac{{11}}{1}{\rm{ }};{\rm{ }}3,111 = \dfrac{{3111}}{{1000}};{\rm{ }}4\dfrac{5}{7}{\rm{ = }}\dfrac{{33}}{7}{\rm{; }}-{\rm{ }}34 = \dfrac{{ – 34}}{1};{\rm{ }}-{\rm{ }}1,3 = \dfrac{{ – 13}}{{10}}\).

Giải bài tập Toán 7 Cánh diều Chương 1 Bài 1

Giải bài 2 trang 9 SBT Toán 7 Cánh diều tập 1

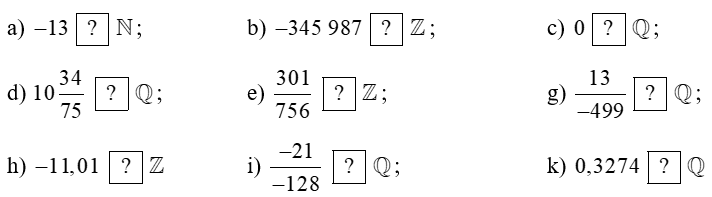
Phương pháp giải:

\(\mathbb{N}=\{{0;1;2;3;…\}}\)

\(\mathbb{Z}=\{{…;-3;-2;-1;0;1;2;3;…\}}\)

\(\mathbb{Q}=\{{\dfrac{a}{b}:a,b \in Z, b\ne0\}}\)

Lời giải chi tiết:

a) – 13 \( \notin \) \(\mathbb{N}\); 

b) – 345 987 \( \in \)\(\mathbb{Z}\);

c) 0 \( \in \)\(\mathbb{Q}\);

d) \(10\dfrac{{34}}{{75}}\)\( \in \)\(\mathbb{Q}\); 

e) \(\dfrac{{301}}{{756}}\)\( \notin \)\(\mathbb{Z}\); 

g) \(\dfrac{{13}}{{ – 499}}\)\( \in \)\(\mathbb{Q}\);

h) – 11, 01\( \notin \)\(\mathbb{Z}\); 

i) \(\dfrac{{ – 21}}{{ – 128}}\)\( \in \)\(\mathbb{Q}\); 

k) 0,3274 \( \in \) \(\mathbb{Q}\).

Giải bài tập Toán 7 Cánh diều Chương 1 Bài 1

Giải bài 3 trang 9 SBT Toán 7 Cánh diều tập 1

Phương pháp giải:

Đọc ý kiến của ba bạn rồi xác định tính đúng sai dự vào:

–        Số hữu tỉ là số viết được dưới dạng phân số \(\dfrac{a}{b}\) với \(a,{\rm{ }}b \in \mathbb{Z},{\rm{ }}b \ne 0\).

–        Mỗi số nguyên là một số hữu tỉ.

Lời giải chi tiết:

– An: “Số 0 là số nguyên và không phải là số hữu tỉ.”

Bạn An phát biểu sai. Vì số 0 vừa là số nguyên vừa là số hữu tỉ. (Số 0 có thể được biểu diễn dưới dạng \(\dfrac{0}{1}\)).

– Bình: “Số hữu tỉ là số được viết dưới dạng phân số \(\dfrac{a}{b}\) với \(a,b \in \mathbb{Z}\).”

Bạn Bình phát biểu sai. Vì cần thêm điều kiện \(b \ne 0\).

– Chi: “Mỗi số nguyên là một số hữu tỉ.”

Bạn Chi phát biểu đúng. Vì mỗi số nguyên \(a\) đều biểu diễn được dưới dạng \(\dfrac{a}{1}\). 

Giải bài tập Toán 7 Cánh diều Chương 1 Bài 1

Giải bài 4 trang 9 SBT Toán 7 Cánh diều tập 1

Phương pháp giải:

Quan sát trục số ở Hình 5 rồi xác định số hữu tỉ \(\dfrac{3}{4}\).

Ta có thể so sánh số được biểu diễn với 0 và 1 hoặc xác định dựa vào cách chia đoạn thẳng đơn vị trên trục số.

Lời giải chi tiết:

Đoạn thẳng đơn vị được chia thành 4 phần bằng nhau. Mỗi phần đó được coi như 1 đơn vị mới.

Khi đó, điểm biểu diễn số hữu tỉ \(\dfrac{3}{4}\) là điểm nằm bên phải điểm 0 và cách điểm 0 một khoảng bằng 3  đơn vị mới.

Điểm biểu diễn số hữu tỉ \(\dfrac{3}{4}\) là điểm C.

Giải bài tập Toán 7 Cánh diều Chương 1 Bài 1

Giải bài 5 trang 9 SBT Toán 7 Cánh diều tập 1

Phương pháp giải:

Số đối của một số a là – a. Tổng của một số và số đối của nó bằng 0.

Lời giải chi tiết:

Số đối của các số hữu tỉ \(\dfrac{{37}}{{221}};{\rm{ }}\dfrac{{ – 93}}{{1171}};{\rm{ }}\dfrac{{87}}{{ – 19543}}; 41,02; – 791,8\) lần lượt là:

\(\dfrac{{ – 37}}{{221}};{\rm{ }}\dfrac{{93}}{{1171}};{\rm{ }}\dfrac{{ 87}}{{ 19543}}; –  41,02; 791,8.\)

Giải bài tập Toán 7 Cánh diều Chương 1 Bài 1

Giải bài 6 trang 9 SBT Toán 7 Cánh diều tập 1

Phương pháp giải:

Xác định số đối của các số hữu tỉ đã cho trên trục số rổi biểu diễn chúng trên trục số.

Lời giải chi tiết:

Số đối của các số hữu tỉ \(\;\dfrac{{ – 9}}{4};{\rm{ }}\dfrac{{ – 7}}{4};{\rm{ }} – 1;{\rm{ }}\dfrac{{ – 1}}{2};{\rm{ }}0;{\rm{ }}1;{\rm{ }}\dfrac{5}{4}\) lần lượt là:

\(\;\dfrac{9}{4};{\rm{ }}\dfrac{7}{4};{\rm{ }}1;{\rm{ }}\dfrac{1}{2};{\rm{ }}0;{\rm{ }} – 1;{\rm{ }}\dfrac{{ – 5}}{4}\).

Chia đoạn thẳng đơn vị thành 4 đoạn thẳng bằng nhau, ta được đơn vị mới bằng \(\dfrac{1}{4}\) đơn vị cũ.

∙ Số hữu tỉ \(\dfrac{9}{4}\) nằm bên phải điểm 0 và cách điểm 0 một khoảng bằng 9 đơn vị mới.

∙ Số hữu tỉ \(\dfrac{7}{4}\) nằm bên phải điểm 0 và cách điểm 0 một khoảng bằng 7 đơn vị mới.

∙ Số hữu tỉ \(\dfrac{1}{2}=\dfrac{2}{4}\) nằm bên phải điểm 0 và cách điểm 0 một khoảng bằng 2 đơn vị mới.

∙ Số hữu tỉ \(\dfrac{-5}{4}\) nằm bên trái điểm 0 và cách điểm 0 một khoảng bằng 5 đơn vị mới.

Biểu diễn số đối của các số hữu tỉ trên trục số:

Giải bài tập Toán 7 Cánh diều Chương 1 Bài 1

Giải bài 7 trang 10 SBT Toán 7 Cánh diều tập 1

Phương pháp giải:

– Khi so sánh hai phân số có cùng tử số dương, mẫu số của phân số nào bé hơn thì phân số đó lớn hơn.

– Khi so sánh hai phân số có cùng tử số âm, mẫu số của phân số nào bé hơn thì phân số đó bé hơn.

Chú ý: Nếu a < b; b < c thì a < c

Lời giải chi tiết:

a) Ta có: \(3,2 = 3 + 0,2 = 3 + \dfrac{2}{{10}} = 3\dfrac{2}{{10}}\).

Do \(\dfrac{2}{{11}} < \dfrac{2}{{10}}\)nên \(3\dfrac{2}{{11}} < 3\dfrac{2}{{10}}\) hay \(3\dfrac{2}{{11}} < 3,2\).

b) Ta có: \(-{\rm{ }}0,01 = \dfrac{{ – 1}}{{100}} = \dfrac{{ – 5}}{{500}}\).

Do 211 < 500 nên \(\dfrac{{ 5}}{{211}} > \dfrac{{5}}{{500}}\). Do đó,\(\dfrac{{ – 5}}{{211}} < \dfrac{{ – 5}}{{500}}\) nên \(\dfrac{{ – 5}}{{211}} <  – 0,01\).

c) Ta có: \(\dfrac{{105}}{{ – 15}} =  – 7\).

Do \( – 7 >  – 7,112\) nên \(\dfrac{{105}}{{ – 15}} >  – 7,112\).

d) Ta có: – 943,001 < 0 < 943,0001.

Nên – 943,001 < 943,0001. 

Giải bài tập Toán 7 Cánh diều Chương 1 Bài 1

Giải bài 8 trang 10 SBT Toán 7 Cánh diều tập 1

Phương pháp giải:

So sánh các cặp số với nhau, từ đó sắp xếp chúng theo thứ tự tăng dần.

Lời giải chi tiết:

a)  \(3\dfrac{2}{{11}};{\rm{ }}2\dfrac{1}{{12}};{\rm{ }}\dfrac{{15}}{{21}};{\rm{ }}\dfrac{{17}}{{21}}\).

Cách 1: Ta có:

Vì 15 < 17 nên \(\dfrac{{15}}{{21}}{\rm{  <  }}\dfrac{{17}}{{21}}\).

\(2\dfrac{1}{{12}} = \dfrac{{25}}{{12}} = \dfrac{{175}}{{84}};{\rm{ }}\dfrac{{17}}{{21}} = \dfrac{{68}}{{84}}\). Do \(\dfrac{{175}}{{84}}{\rm{  > }}\,{\rm{ }}\dfrac{{68}}{{84}}\) nên \(2\dfrac{1}{{12}} > \dfrac{{17}}{{21}}\).

\(3\dfrac{2}{{11}} = \dfrac{{35}}{{11}} = \dfrac{{420}}{{132}};{\rm{ 2}}\dfrac{1}{{12}} = \dfrac{{25}}{{12}} = \dfrac{{275}}{{132}}\). Do \(\dfrac{{420}}{{132}}{\rm{  >  }}\dfrac{{275}}{{132}}\) nên \(3\dfrac{2}{{11}}{\rm{  >  2}}\dfrac{1}{{12}}\).

Suy ra: \(\dfrac{{15}}{{21}}{\rm{  <  }}\dfrac{{17}}{{21}}{\rm{  <  }}2\dfrac{1}{{12}}{\rm{  <  }}3\dfrac{2}{{11}}\).

Các số theo thứ tự tăng dần: \(\dfrac{{15}}{{21}}{\rm{; }}\dfrac{{17}}{{21}}{\rm{; }}2\dfrac{1}{{12}}{\rm{; }}3\dfrac{2}{{11}}\).

Cách 2:

Vì 15 < 17 nên \(\dfrac{{15}}{{21}}{\rm{  <  }}\dfrac{{17}}{{21}}\).

Ta có: \(\dfrac{{15}}{{21}}{\rm{  <  }}\dfrac{{17}}{{21}}<1<2\dfrac{1}{{12}}<3<3\dfrac{2}{{11}}\)

Ta được: \(\dfrac{{15}}{{21}}{\rm{  <  }}\dfrac{{17}}{{21}}{\rm{  <  }}2\dfrac{1}{{12}}{\rm{  <  }}3\dfrac{2}{{11}}\).

Các số theo thứ tự tăng dần: \(\dfrac{{15}}{{21}}{\rm{; }}\dfrac{{17}}{{21}}{\rm{; }}2\dfrac{1}{{12}}{\rm{; }}3\dfrac{2}{{11}}\).

b) – 5,12; 0,534; – 23; 123; 0; 0,543.

Ta có: \(-{\rm{ }}5,12;{\rm{ }}-23 < {\rm{ }}0{\rm{ }} < {\rm{ 0,534; 123; 0,543}}\).

Do: \(-{\rm{ }}5,12{\rm{  > }}-23;{\rm{ 0,534  <  0,543  <  123}}\).

Nên \(-23 <  – 5,12 < 0 < {\rm{0,534  <  0,543  < }}\,{\rm{123}}\).

Các số theo thứ tự tăng dần: \(-23; – 5,12;{\rm{ }}0;{\rm{ 0,534; 0,543; 123}}\). 

Giải bài tập Toán 7 Cánh diều Chương 1 Bài 1

Giải bài 9 trang 10 SBT Toán 7 Cánh diều tập 1

Phương pháp giải:

So sánh các cặp số với nhau để sắp xếp chúng theo thứ tự giảm dần.

Lời giải chi tiết:

a) Ta có:

\(\dfrac{2}{{15}};{\rm{ }}\dfrac{2}{3};{\rm{ }}\dfrac{5}{6}{\rm{  >  0  >  }} – \dfrac{7}{8};{\rm{ }}\dfrac{{ – 7}}{9}\).

\( – \dfrac{7}{8} = \dfrac{{ – 7}}{8} < \dfrac{{ – 7}}{9}\);

\(\dfrac{2}{{15}} = \dfrac{8}{{60}};{\rm{ }}\dfrac{2}{3} = \dfrac{{40}}{{60}};{\rm{ }}\dfrac{5}{6}{\rm{ = }}\dfrac{{50}}{{60}}{\rm{ }}\) mà \(\dfrac{8}{{60}} < \dfrac{{40}}{{60}} < \dfrac{{50}}{{60}}\) nên \(\dfrac{2}{{15}} < \dfrac{2}{3} < \dfrac{5}{6}\).

Suy ra: \(\dfrac{5}{6}{\rm{  >  }}\dfrac{2}{3}{\rm{  >  }}\dfrac{2}{{15}}{\rm{  >  }}\dfrac{{ – 7}}{9}{\rm{  > }}\,{\rm{ }} – \dfrac{7}{8}\).

Các số theo thứ tự giảm dần là: \(\dfrac{5}{6};{\rm{ }}\dfrac{2}{3}{\rm{; }}\dfrac{2}{{15}};{\rm{ }}\dfrac{{ – 7}}{9};\,{\rm{ }} – \dfrac{7}{8}\).

b) Cách 1:

Ta có:

\(\dfrac{{19}}{{22}};{\rm{ }}0,5;{\rm{ }}2\dfrac{1}{6}{\rm{  >  0  > }} – \dfrac{1}{4};{\rm{ }} – 0,05\).

\( – \dfrac{1}{4} =  – 0,25 <  – 0,05\).

\(\dfrac{{19}}{{22}} = \dfrac{{57}}{{66}};{\rm{ }}0,5 = \dfrac{1}{2} = \dfrac{{33}}{{66}};{\rm{ }}2\dfrac{1}{6}{\rm{ = }}\dfrac{{13}}{6}{\rm{ = }}\dfrac{{143}}{{66}}{\rm{ }}\)mà \(\dfrac{{33}}{{66}}{\rm{  <  }}\dfrac{{57}}{{66}}{\rm{  <  }}\dfrac{{143}}{{66}}{\rm{ }}\)nên \(0,5{\rm{  <  }}\dfrac{{19}}{{22}}{\rm{  <  2}}\dfrac{1}{6}\).

Suy ra: \({\rm{ }}2\dfrac{1}{6}{\rm{  > }}\,{\rm{ }}\dfrac{{19}}{{22}}{\rm{  >  }}0,5{\rm{  > }} – 0,05{\rm{  >  }} – \dfrac{1}{4}\).

Các số theo thứ tự giảm dần là: \({\rm{ }}2\dfrac{1}{6};\,{\rm{ }}\dfrac{{19}}{{22}}{\rm{; }}0,5;{\rm{ }} – 0,05;{\rm{ }} – \dfrac{1}{4}\). 

Cách 2:

\(\dfrac{{19}}{{22}};{\rm{ }}0,5;{\rm{ }}2\dfrac{1}{6}{\rm{  >  0  > }} – \dfrac{1}{4};{\rm{ }} – 0,05\).

\( – \dfrac{1}{4} =  – 0,25 <  – 0,05\).

\(0,5=\dfrac{11}{22}<\dfrac{19}{22}<1<2\dfrac{1}{6}\)

Ta được: 

\({\rm{ }}2\dfrac{1}{6}{\rm{  > }}\,{\rm{ }}\dfrac{{19}}{{22}}{\rm{  >  }}0,5{\rm{  > }} – 0,05{\rm{  >  }} – \dfrac{1}{4}\).

Các số theo thứ tự giảm dần là: \({\rm{ }}2\dfrac{1}{6};\,{\rm{ }}\dfrac{{19}}{{22}}{\rm{; }}0,5;{\rm{ }} – 0,05;{\rm{ }} – \dfrac{1}{4}\). 

Giải bài tập Toán 7 Cánh diều Chương 1 Bài 1

Giải bài 10 trang 10 SBT Toán 7 Cánh diều tập 1

Phương pháp giải:

a) y là số nguyên khi và chỉ khi 2a – 4 chia hết cho 3.

b) y không là số hữu tỉ âm cũng không là số hữu tỉ dương thì \(y = 0\).

Lời giải chi tiết:

a) y là số nguyên khi và chỉ khi 2a – 4 chia hết cho 3 hay \(2(a – 2) \vdots 3\).

Mà ƯCLN (2, 3) = 1 nên \((a – 2) \vdots 3\).

Suy ra: \(a – 2 = 3k\) (\(k \in \mathbb{Z}\)).

Hay \(a = 3k + 2\).

Vậy để y là số nguyên thì a là số chia cho 3 dư 2.

b) y không là số hữu tỉ âm cũng không là số hữu tỉ dương thì \(y = 0\).

\(\Leftrightarrow 2a – 4 = 0 \Leftrightarrow a = 2\).

Vậy để y không là số hữu tỉ âm cũng không là số hữu tỉ dương thì \(a = 2\). 

Giải bài tập Toán 7 Cánh diều Chương 1 Bài 1