Giải bài tập Bài 2: Biểu thức tọa độ của các phép toán vectơ (C7 – Toán 10 Cánh diều)
0000000000000000000000
Giải bài tập Bài 1 trang 72 SGK Toán 10 Cánh diều tập 2
Trong mặt phẳng tọa độ Oxy, cho \(\overrightarrow a = \left( { – 1;2} \right),\overrightarrow b = \left( {3;1} \right),\overrightarrow c = \left( {2; – 3} \right)\).
a) Tìm tọa độ của vectơ \(\overrightarrow u = 2\overrightarrow a + \overrightarrow b – 3\overrightarrow c \)
b) Tìm tọa độ của vectơ \(\overrightarrow x \) sao cho \(\overrightarrow x + 2\overrightarrow b = \overrightarrow a + \overrightarrow c \)
Phương pháp giải
Cho hai vectơ \(\overrightarrow u = \left( {{x_1},{y_1}} \right)\) và \(\overrightarrow v = \left( {{x_2},{y_2}} \right)\) thì: \(\overrightarrow u + \overrightarrow v = \left( {{x_1} + {x_2};{y_1} + {y_2}} \right)\), \(\overrightarrow u – \overrightarrow v = \left( {{x_1} – {x_2};{y_1} – {y_2}} \right)\),\(k\overrightarrow u = \left( {k{x_1},k{y_1}} \right),\left( {k \in \mathbb{R}} \right)\)
Hướng dẫn giải
a) Tọa độ vectơ \(\overrightarrow u = \left( {2.\left( { – 1} \right) + 3 – 3.2;2.2 + 1 – 3.\left( { – 3} \right)} \right) = \left( { – 5;14} \right)\)
b) Do \(\overrightarrow x + 2\overrightarrow b = \overrightarrow a + \overrightarrow c \Leftrightarrow \overrightarrow x = \overrightarrow a + \overrightarrow c – 2\overrightarrow b = \left( { – 1 + 2 – 2.3;2 + \left( { – 3} \right) – 2.1} \right) = \left( { – 5; – 3} \right)\)
Vậy \(\overrightarrow x = \left( { – 5; – 3} \right)\)
Giải bài tập Bài 2 trang 72 SGK Toán 10 Cánh diều tập 2
Trong mặt phẳng toạ độ Oxy, cho A(-2;3), B(4; 5), C(2;- 3).
a) Chứng minh ba điểm A, B, C không thẳng hàng.
b) Tìm toạ độ trọng tâm G của tam giác ABC.
c) Giải tam giác ABC (làm tròn các kết quả đến hàng đơn vị).
Phương pháp giải
a) Hai vectơ \(\overrightarrow u = \left( {{x_1},{y_1}} \right)\), \(\overrightarrow v = \left( {{x_2},{y_2}} \right)\) (\(\overrightarrow v \ne 0\) ) cùng phương khi và chỉ khi có một số thực k sao cho \({x_1}{\rm{ = }}k{x_2}\) và \({y_1} = {\rm{ }}k{y_2}\) .
b) G là trọng tâm tam giác ABC thì tọa độ G là: \(G\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)\)
c) Tính tất cả các cạnh và các góc của tam giác ABC:
Nếu \(\overrightarrow a = \left( {x;y} \right) \Rightarrow \left| {\overrightarrow a } \right| = \sqrt {{x^2} + {y^2}} \)
Với hai vectơ \(\overrightarrow u = \left( {{x_1},{y_1}} \right)\), \(\overrightarrow v = \left( {{x_2},{y_2}} \right)\)đều khác vectơ không, ta có:
+ \(\overrightarrow u \) và \(\overrightarrow v \) vuông góc với nhau khi và chỉ khi \({x_1}.{x_2} + {y_1}.{y_2} = 0\)
+ \(\cos \left( {\overrightarrow u ,\overrightarrow v } \right) = \frac{{\overrightarrow u .\overrightarrow v }}{{\left| {\overrightarrow u } \right|\left| {\overrightarrow v } \right|}} = \frac{{{x_1}.{x_2} + {y_1}.{y_2}}}{{\sqrt {x_1^2 + y_1^2} .\sqrt {x_2^2 + y_2^2} }}\)
Hướng dẫn giải
a) Ta có: \(\overrightarrow {AB} = \left( {6;2} \right),\overrightarrow {AC} = \left( {4; – 6} \right)\)
Do \(\overrightarrow {AB} \ne k.\overrightarrow {AC} \) nên A, B, C không thẳng hàng
b) Do G là trọng tâm tam giác ABC nên \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3} = \frac{{ – 2 + 4 + 2}}{3} = \frac{4}{3}\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{{3 + 5 + \left( { – 3} \right)}}{3} = \frac{5}{3}\end{array} \right.\)
Vậy \(G\left( {\frac{4}{3};\frac{5}{3}} \right)\)
c) Ta có: \(\overrightarrow {AB} = \left( {6;2} \right),\overrightarrow {AC} = \left( {4; – 6} \right),\overrightarrow {BC} = \left( { – 2; – 8} \right)\)
Suy ra: \(\begin{array}{l}AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{6^2} + {2^2}} = \sqrt {40} \\AC = \left| {\overrightarrow {AC} } \right| = \sqrt {{4^2} + {{\left( { – 6} \right)}^2}} = \sqrt {52} \\BC = \left| {\overrightarrow {BC} } \right| = \sqrt {{{\left( { – 2} \right)}^2} + {{\left( { – 8} \right)}^2}} = \sqrt {68} \end{array}\)
Ta có:
\(\begin{array}{l}\cos \widehat {BAC} = \cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \frac{{6.4 + 2.\left( { – 6} \right)}}{{\sqrt {{6^2} + {2^2}} .\sqrt {{4^2} + {{\left( { – 6} \right)}^2}} }} \approx 0,263 \Rightarrow \widehat {BAC} \approx {74^o}\\\cos \widehat {ABC} = \cos \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) = \frac{{\left( { – 6} \right).\left( { – 2} \right) + \left( { – 2} \right).\left( { – 8} \right)}}{{\sqrt {{{\left( { – 6} \right)}^2} + {{\left( { – 2} \right)}^2}} .\sqrt {{{\left( { – 2} \right)}^2} + {{\left( { – 8} \right)}^2}} }} \approx 0,47 \Rightarrow \widehat {ABC} \approx {62^o}\end{array}\)
Áp dụng tính chất tổng ba góc trong một tam giác ta có: \(\widehat {ACB} \approx {180^o} – {74^o} – {62^o} \approx {44^o}\)
Giải bài tập Bài 3 trang 72 SGK Toán 10 Cánh diều tập 2
Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có trung điểm các cạnh BC, CA, AB tương ứng là M(2 ; 0), N4 ; 2), P(1 ; 3).
a) Tìm toạ độ các điểm A, B, C.
b) Trọng tâm hai tam giác ABC và MNP có trùng nhau không? Vì sao?
Phương pháp giải
a) Trung điểm M của đoạn thẳng AB có tọa độ là: \(M\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)
b) Tìm trọng tâm của hai tam giác bằng công thức tính trọng tâm: G là trọng tâm tam giác ABC thì tọa độ G là: \(G\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)\)
Hướng dẫn giải
a) Do M, N, P là trung điểm của các cạnh BC, CA, AB nên:
\(\left\{ \begin{array}{l}\frac{{{x_B} + {x_C}}}{2} = {x_M}\\\frac{{{x_B} + {x_A}}}{2} = {x_P}\\\frac{{{x_A} + {x_C}}}{2} = {x_N}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} + {x_C} = 4\\{x_B} + {x_A} = 2\\{x_A} + {x_C} = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_A} = 3\\{x_B} = – 1\\{x_C} = 5\end{array} \right.\) và \(\left\{ \begin{array}{l}\frac{{{y_B} + {y_C}}}{2} = {y_M}\\\frac{{{y_B} + {y_A}}}{2} = {y_P}\\\frac{{{y_A} + {y_C}}}{2} = {y_N}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{y_B} + {y_C} = 0\\{y_B} + {y_A} = 4\\{y_A} + {y_C} = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{y_A} = 5\\{y_B} = – 1\\{y_C} = 1\end{array} \right.\)
Vậy \(A\left( {3;5} \right),B\left( { – 1; – 1} \right),C\left( {5;1} \right)\)
b) Trọng tâm tam giác ABC có tọa độ là: \(\left\{ \begin{array}{l}\frac{{{x_A} + {x_B} + {x_C}}}{3} = \frac{{3 + \left( { – 1} \right) + 5}}{3} = \frac{7}{3}\\\frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{{5 + \left( { – 1} \right) + 1}}{3} = \frac{5}{3}\end{array} \right.\)
Trọng tâm tam giác MNP có tọa độ là: \(\left\{ \begin{array}{l}\frac{{{x_M} + {x_N} + {x_P}}}{3} = \frac{{2 + 4 + 1}}{3} = \frac{7}{3}\\\frac{{{y_M} + {y_N} + {y_P}}}{3} = \frac{{0 + 2 + 3}}{3} = \frac{5}{3}\end{array} \right.\)
Vậy trọng tâm của 2 tam giác ABC và MNP là trùng nhau vì có cùng tọa độ.
Giải bài tập Bài 4 trang 72 SGK Toán 10 Cánh diều tập 2
Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có A(2;4), B(-1;1), C(-8; 2).
a) Tính số đo góc ABC (làm tròn kết quả đến hàng đơn vị theo đơn vị độ).
b) Tính chu vi của tam giác ABC.
c) Tìm toạ độ điểm M trên đường thẳng BC sao cho diện tích của tam giác ABC bằng hai lần diện tích của tam giác ABM.
Phương pháp giải
a) Với hai vectơ \(\overrightarrow u = \left( {{x_1},{y_1}} \right)\), \(\overrightarrow v = \left( {{x_2},{y_2}} \right)\)đều khác vectơ không, ta có:
– \(\overrightarrow u \) và \(\overrightarrow v \) vuông góc với nhau khi và chỉ khi \({x_1}.{x_2} + {y_1}.{y_2} = 0\)
– \(\cos \left( {\overrightarrow u ,\overrightarrow v } \right) = \frac{{\overrightarrow u .\overrightarrow v }}{{\left| {\overrightarrow u } \right|\left| {\overrightarrow v } \right|}} = \frac{{{x_1}.{x_2} + {y_1}.{y_2}}}{{\sqrt {x_1^2 + y_1^2} .\sqrt {x_2^2 + y_2^2} }}\)
b) Chu vi tam giác bằng tổng độ dài 3 cạnh
c) Trung điểm M của đoạn thẳng AB có tọa độ là: \(M\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)
Hướng dẫn giải
a) Ta có: \(\overrightarrow {BC} = \left( { – 7;1} \right),\overrightarrow {BA} = \left( {3;3} \right)\)
\(\cos \widehat {ABC} = \left( {\overrightarrow {BC} ,\overrightarrow {BA} } \right) = \frac{{\left( { – 7} \right).3 + 1.3}}{{\sqrt {{{\left( { – 7} \right)}^2} + {1^2}} .\sqrt {{3^2} + {3^2}} }} = – \frac{3}{5} \Rightarrow \widehat {ABC} \approx {126^o}\)
b) Ta có: \(\overrightarrow {BC} = \left( { – 7;1} \right),\overrightarrow {BA} = \left( {3;3} \right),\overrightarrow {AC} = \left( { – 10; – 2} \right)\)
Suy ra: \(\begin{array}{l}AB = \left| {\overrightarrow {BA} } \right| = \sqrt {{3^2} + {3^2}} = 3\sqrt 2 \\AC = \left| {\overrightarrow {AC} } \right| = \sqrt {{{\left( { – 10} \right)}^2} + {{\left( { – 2} \right)}^2}} = \sqrt {104} \\BC = \left| {\overrightarrow {BC} } \right| = \sqrt {{{\left( { – 7} \right)}^2} + {1^2}} = \sqrt {50} \end{array}\)
Vậy chu vi tam giác ABC là: \({P_{ABC}} = 2\sqrt {26} + 8\sqrt 2 \)
c) Để diện tích của tam giác ABC bằng hai lần diện tích của tam giác ABM thì M phải là trung điểm BC.
Vậy tọa độ điểm M là: \(\left\{ \begin{array}{l}\frac{{{x_B} + {x_C}}}{2} = \frac{{ – 9}}{2}\\\frac{{{y_B} + {y_C}}}{2} = \frac{3}{2}\end{array} \right.\). Vậy \(M\left( {\frac{{ – 9}}{2};\frac{3}{2}} \right)\)
Giải bài tập Bài 5 trang 72 SGK Toán 10 Cánh diều tập 2
Cho ba điểm A(1; 1), B(4;3) và C(0;- 2).
a) Chứng minh ba điểm A, B, C không thẳng hàng.
b) Tìm toạ độ điểm D sao cho tứ giác ABCD là hình thang có AB // CD và CD= 2AB.
Phương pháp giải
a) Hai vectơ \(\overrightarrow u = \left( {{x_1},{y_1}} \right)\), \(\overrightarrow v = \left( {{x_2},{y_2}} \right)\) (\(\overrightarrow v \ne 0\) ) cùng phương khi và chỉ khi có một số thực k sao cho \({x_1}{\rm{ = }}k{x_2}\) và \({y_1} = {\rm{ }}k{y_2}\) .
b) Tứ giác ABCD là hình thang có AB // CD và CD= 2AB thì 2 vectơ \(\overrightarrow {AB} ,\overrightarrow {CD} \) phải cùng phương và độ lớn vectơ \(\overrightarrow {CD} = 2\overrightarrow {AB} \)
Hướng dẫn giải
a) Ta có: \(\overrightarrow {AB} = \left( {3;2} \right),\overrightarrow {AC} = \left( { – 1; – 3} \right)\)
Do \(\overrightarrow {AB} \ne k.\overrightarrow {AC} \) nên A, B, C không thẳng hàng
b) Giả sử tọa độ điểm D là:\(D\left( {{x_D},{y_D}} \right)\)
Ta có: \(\overrightarrow {CD} = \left( {{x_D} – 0;{y_D} – \left( { – 2} \right)} \right) = \left( {{x_D};{y_D} + 2} \right)\)
Để tứ giác ABCD là hình thang có AB // CD và CD= 2AB thì \(\overrightarrow {CD} = 2\overrightarrow {AB} \)
Vậy nên \(\overrightarrow {CD} = 2\overrightarrow {AB} \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 2.3\\{y_D} + 2 = 2.2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 6\\{y_D} = 2\end{array} \right.\)
Vậy tọa độ D là: \(D\left( {6;2} \right)\)
Giải bài tập Bài 6 trang 72 SGK Toán 10 Cánh diều tập 2
Chứng minh khẳng định sau: Hai vectơ \(\overrightarrow u = \left( {{x_1},{y_1}} \right)\), \(\overrightarrow v = \left( {{x_2},{y_2}} \right)\) (\(\overrightarrow v \ne 0\) ) cùng phương khi và chỉ khi có một số thực k sao cho \({x_1}{\rm{ = }}k{x_2}\) và \({y_1} = {\rm{ }}k{y_2}\) .
Phương pháp giải
Hai vectơ cùng phương thì tồn tại một số \(k\left( {k \in \mathbb{R}} \right)\) sao cho vectơ này bằng \(k\) lần vectơ kia.
Hướng dẫn giải
Để hai vectơ \(\overrightarrow u = \left( {{x_1},{y_1}} \right)\), \(\overrightarrow v = \left( {{x_2},{y_2}} \right)\) (\(\overrightarrow v \ne 0\) ) cùng phương thì phải tồn tại một số \(k\left( {k \in \mathbb{R}} \right)\) sao cho \(\overrightarrow u = k.\overrightarrow v \Leftrightarrow \left\{ \begin{array}{l}{x_1} = k{x_2}\\{y_1} = k{y_2}\end{array} \right.\) ( ĐPCM)
Giải bài tập Bài 7 trang 72 SGK Toán 10 Cánh diều tập 2
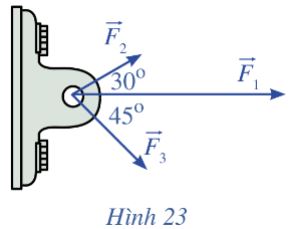
Một vật đồng thời bị ba lực tác động: lực tác động thứ nhất \(\overrightarrow {{F_1}} \) có độ lớn là 1 500 N, lực tác động thứ hai\(\overrightarrow {{F_2}} \) , có độ lớn là 600 N, lực tác động thứ ba\(\overrightarrow {{F_3}} \) , có độ lớn là 800 N. Các lực này được biểu diễn bằng những vectơ như Hình 23, với \(\left( {\overrightarrow {{F_1}} ,{\rm{ }}\overrightarrow {{F_2}} } \right)\) = 30°, \(\left( {\overrightarrow {{F_1}} ,{\rm{ }}\overrightarrow {{F_3}} } \right)\)= 45° và \(\left( {\overrightarrow {{F_2}} ,{\rm{ }}\overrightarrow {{F_3}} } \right)\)= 75°. Tính độ lớn lực tổng hợp tác động lên vật (làm tròn kết quả đến hàng đơn vị).

Phương pháp giải
Chọn hệ trục tọa độ Oxy như hình vẽ
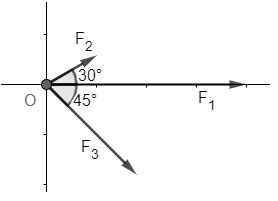
Hướng dẫn giải
Ta có: \(\overrightarrow {{F_1}} = \left( {1500;0} \right)\)
Do \(\;\left( {\overrightarrow {{F_1}} ,{\rm{ }}\overrightarrow {{F_2}} } \right) = 30^\circ \) nên tọa độ của \(\overrightarrow {{F_2}} \)là: \(\overrightarrow {{F_2}} = \left( {600.\cos {{30}^o};600.\sin {{30}^o}} \right) = \left( {300\sqrt 3 ;300} \right)\)
Do \(\left( {\overrightarrow {{F_1}} ,{\rm{ }}\overrightarrow {{F_3}} } \right) = {45^o}\) nên tọa độ của \(\overrightarrow {{F_3}} \)là: \(\overrightarrow {{F_3}} = \left( {800.\cos {{45}^o}; – 800.\sin {{45}^o}} \right) = \left( {400\sqrt 2 ; – 400\sqrt 2 } \right)\)
Do đó, lực \(\overrightarrow F \) tổng hợp các lực tác động lên vật có tọa độ là: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \left( {1500 + 300\sqrt 3 + 400\sqrt 2 ;300 – 400\sqrt 2 } \right)\)
Độ lớn lực tổng hợp \(\overrightarrow F \) tác động lên vật là: \(\left| {\overrightarrow F } \right| = \sqrt {{{\left( {1500 + 300\sqrt 3 + 400\sqrt 2 } \right)}^2} + {{\left( {300 – 400\sqrt 2 } \right)}^2}} \approx 2599\left( N \right)\)
