Để loại bỏ $x%$ chất gây ô nhiễm môi trường từ khí thải của một nhà máy, người ta ước tính chi phí (triệu đồng) cần bỏ ra được mô hình hóa bởi hàm số có dạng $C\left( x \right)=\dfrac{ax+b}{-x+d}$ (như hình vẽ), $\left( 0\le x{<}100 \right)$

Để loại bỏ $x

Lời giải

Đáp án: 18.

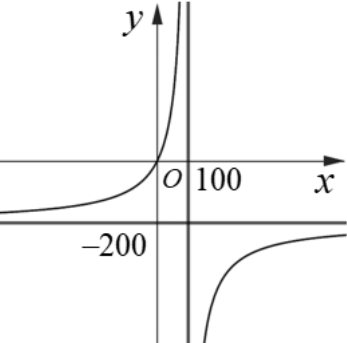
Từ đồ thị hàm số ta thấy: Đồ thị đi qua gốc tọa độ nên $b=0$.

Đồ thị có đường tiệm cận đứng $x=100\Rightarrow d=100$.

Đồ thị có đường tiệm cận ngang $y=-200\Rightarrow -a=-200\Rightarrow a=200$.

Vậy ta có $C\left( x \right)=\dfrac{200x}{-x+100}$.

Suy ra chi phí chênh lệch (tỉ đồng) phải bỏ ra để loại bỏ $90

$C\left( 99 \right)-C\left( 90 \right)=\dfrac{200.99}{-99+100}-\dfrac{200.90}{-90+100}=18000$ (triệu đồng) $=18$ tỉ đồng.