Giả sử chi phí đặt hàng và vận chuyển $C$ (đơn vị: triệu đồng) của một linh kiện được sử dụng trong sản xuất một sản phầm được xác định theo công thức $C=\dfrac{19200000}{{{x}^{2}}}+\dfrac{27x}{x+3000},x\ge 1$. Trong đó $x$ là số linh kiện được đặt hàng và vận chuyển. Tìm $x$ để chi phí đặt hàng và vận chuyển cho mỗi linh kiện trên là nhỏ nhất.
Lời giải
Đáp án: $2400$.
Xét hàm số $C\left( x \right)=\dfrac{19200000}{{{x}^{2}}}+\dfrac{27x}{x+3000},x\ge 1$
Ta có ${C}’\left( x \right)=-\dfrac{38400000}{{{x}^{3}}}+\dfrac{81000}{{{\left( x+3000 \right)}^{2}}}$
${C}’\left( x \right)=0\Leftrightarrow \dfrac{38400000}{{{x}^{3}}}=\dfrac{81000}{{{\left( x+3000 \right)}^{2}}}$
$\Leftrightarrow 12800{{\left( x+3000 \right)}^{2}}=27{{x}^{3}}\Leftrightarrow x=2400$.
Ta có bảng biến thiên
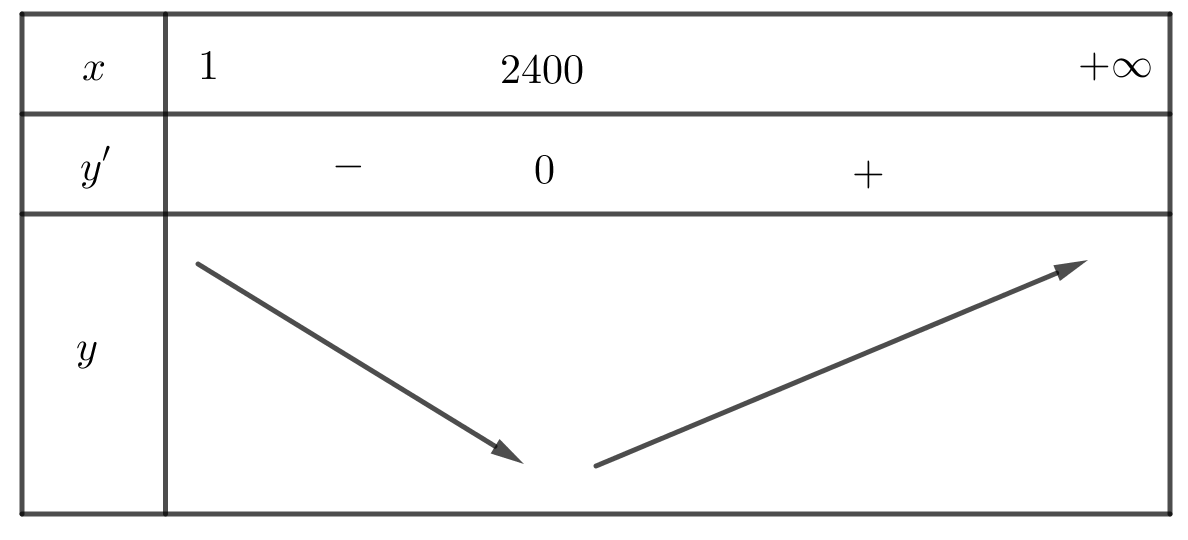
Vậy chi phí đặt hàng và vận chuyển cho mỗi linh kiện trên là nhỏ nhất khi $x=2400$.
