Một doanh nghiệp dự định sản xuất không quá 500 sản phẩm. Nếu doanh nghiệp sản xuất ${x}$ sản phẩm ( ${1 \le x \le 500}$ ) thì doanh thu nhận được khi bán hết số sản phẩm đó là ${F(x) = x^3 – 1999x^2 + 1001000x + 250000}$ (đồng), trong khi chi phí sản xuất bình quân cho một sản phẩm là ${G(x) = x + 1000 + \dfrac{250000}{x}}$ (đồng). Doanh nghiệp cần sản xuất bao nhiêu sản phẩm để lợi nhuận thu được là lớn nhất?
Lời giải
Đáp án: 333.
Ta xét hàm lợi nhuận nếu doanh nghiệp sản xuất ${x}$ sản phẩm ( ${1 \le x \le 500}$ ) là: $f(x)=F(x)-x.G(x)={{x}^{3}}-1999{{x}^{2}}+1001000x+250000-x\left( x+1000+\dfrac{250000}{x} \right)$
$={{x}^{3}}-2000{{x}^{2}}+1000000x$;
${f}'(x)=3{{x}^{2}}-4000x+1000000$;
${f}'(x)=0\Leftrightarrow \left[ \begin{array}{l}
x=\dfrac{1000}{3}\approx 333,33\in \left[ 1;500 \right] \\
x=1000\notin \left[ 1;500 \right] \\
\end{array} \right.$.
Ta lập bảng biến thiên của hàm số trên đoạn $\left[ 1;500 \right]$
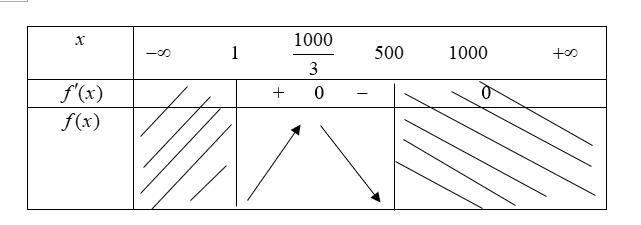
Từ bảng biến thiên, ta có: $\max\limits_{\left[ 1;500 \right]} f(x)=f\left( \dfrac{1000}{3} \right)\approx 148148148$.
Vì ${x}$ là số tự nhiên, nên ta tính thêm hai giá trị của ${x}$ liền kề $\dfrac{1000}{3}$ :
$f\left( 333 \right)\approx 148148037;f\left( 334 \right)\approx 148147704.$
Do đó doanh nghiệp lợi nhuận thu được là lớn nhất khi sản xuất 333 sản phẩm.
