Một xưởng thủ công mỹ nghệ sản xuất loại chụp đèn trang trí dạng hình chóp cụt tứ giác đều. Gọi $x$ là độ dài cạnh đáy lớn (đơn vị:dm). Tính toán cho thấy tổng chi phí vật liệu (tính bằng nghìn đồng) cho một chụp đèn là $C\left( x \right)={{x}^{2}}+108$ (nghìn đồng). Thời gian sản xuất cho một chụp đèn được xác định là $T\left( x \right)=x+6$ (giờ). Xưởng muốn xác định kích thước $x$ để chi phí vật liệu trung bình trên một giờ sản xuất là thấp nhất, nhằm tối ưu hóa hiệu quả sử dụng thời gian và vật liệu. Hãy tìm giá trị của $x$.
Lời giải
Đán án: 6
Gọi hàm chi phí vật liệu trung bình trên một giờ sản xuất là $f\left( x \right)=\dfrac{C\left( x \right)}{T\left( x \right)}=\dfrac{{{x}^{2}}+108}{x+6},x{>}0$.
Ta có $f’\left( x \right)=\dfrac{{{x}^{2}}+12x-108}{{{\left( x+6 \right)}^{2}}}=0\Leftrightarrow \left[ \begin{array}{l}
x=-18(L) \\
x=6 \\
\end{array} \right.$
Ta có bảng biến thiên :
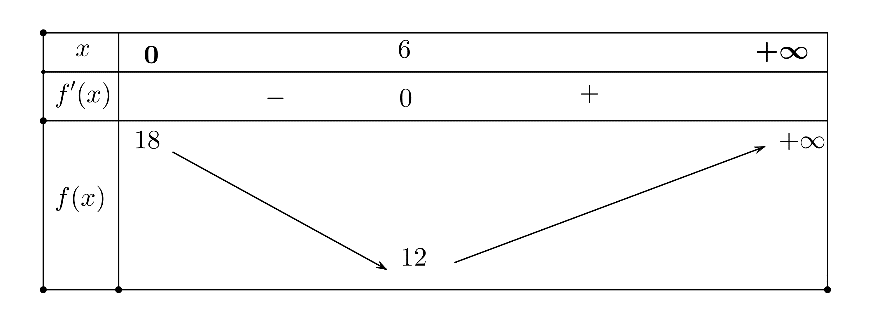
Từ bảng biến thiên ta thấy $f\left( x \right)$ đạt GTNN bằng $12$ khi $x=6$.
Vậy để chi phí vật liệu trung bình trên một giờ sản xuất là thấp nhất thì $x=6$.
