Để tạo một kiện hàng dạng hình lăng trụ đứng với đáy là hình chữ nhật có chiều dài gấp đôi chiều rộng, người ta dùng các thanh gỗ ghép khít đóng lại với nhau. Biết rằng, dung tích kiện hàng bằng $9{{\text{m}}^{\text{3}}}$ và giá thành $1{{\text{m}}^{\text{2}}}$ gỗ sử dụng là $200000$ đồng. Hỏi sau khi hoàn thành kiện hàng đó, người ta cần bỏ ra ít nhất bao nhiêu triệu đồng? (diện tích các mép giữa hai mặt kề nhau không đáng kể).

Lời giải
Đáp án: $5,4$.
Gọi $x\left( x{>}0 \right)$ là chiều rộng của đáy bể. Khi đó chiều dài của kiện hàng là $2x$ là chiều cao của kiện hàng là $\dfrac{9}{2{{x}^{2}}}$. Khi đó diện tích của kiện hàng là $4{{x}^{2}}+\dfrac{27}{x}$
Xét hàm số $f\left( x \right)=4{{x}^{2}}+\dfrac{27}{x}$ có ${f}’\left( x \right)=8x-\dfrac{27}{{{x}^{2}}}=0\Leftrightarrow x=1,5$
Bảng biến thiên của hàm số $f\left( x \right)$ như sau:
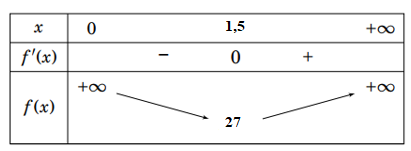
Từ bảng biên thiên ta có $\min f\left( x \right)=f\left( 1,5 \right)=27$ Vậy chi phí thấp nhất làm kiện hàng là: $200000.27=5400000$ đồng.
