Một hộp không nắp được làm từ một mảnh các tông theo hình vẽ. Hộp có đáy là một hình vuông cạnh $x\left( \text{cm} \right)$, chiều cao là $h\left( \text{cm} \right)$ và thể tích là $4000\text{c}{{\text{m}}^{\text{3}}}$. Tìm $x\left( \text{cm} \right)$ sao cho chiếc hộp làm ra tốn ít bìa các tông nhất.
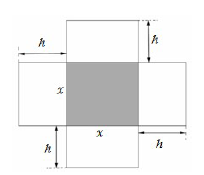
Lời giải
Đáp án: 20.
Điều kiện $x{>}0$
Ta có thể tích của chiếc hộp là $V={{x}^{2}}.h$
Theo giả thiết thể tích chiếc hộp bằng $4000\text{c}{{\text{m}}^{\text{3}}}$ nên ta có ${{x}^{2}}.h=4000\Leftrightarrow h=\dfrac{4000}{{{x}^{2}}}$
Ta có diện tích xung quanh và đáy của chiếc hộp là $S={{x}^{2}}+4xh={{x}^{2}}+4x.\dfrac{4000}{{{x}^{2}}}={{x}^{2}}+\dfrac{16000}{x}$
Ta khảo sát hàm số $f\left( x \right)={{x}^{2}}+\dfrac{16000}{x}$
Ta có ${f}’\left( x \right)=2x-\dfrac{16000}{{{x}^{2}}}$, ${f}’\left( x \right)=0\Leftrightarrow x=20$
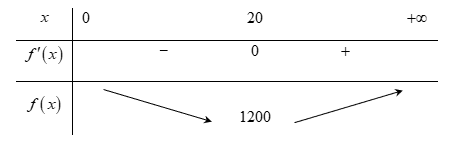
Ta có $x=20\left( \text{cm} \right)$ thì chiếc hộp làm ra tốn ít bìa nhất.
