Một con cá hồi bơi ngược dòng (từ nơi sinh sống) vượt khoảng cách $300km$ để tới nơi sinh sản. Vận tốc dòng nước là $6km/h$. Giả sử vận tốc hơi của cả khi mước đứng yên là $vkm/h$ thì năng lượng tiêu hao của cả trong $t$ giờ cho bởi công thức $E\left( v \right)=c{{v}^{3}}t$ trong đó $c$ là hàng số cho trước. $E$ tính hằng Jun. Tình vận tốc bơi của cả khi nước đứng yên, để năng lượng của cả tiêu hao ít nhất?

Lời giải
Trả lời: 9
Theo đề bài, vận tốc của cá khi bơi trên sông là $v-6$, khi đó thời gian để cá bơi đến nơi sinh sản là $t=\dfrac{300}{v-6}$.
Khi đó, $E\left( v \right)=c{{v}^{3}}\dfrac{300}{v-6}$ với $v{>}6$. Đặt $x=v-6$.
Bài năng lượng tiêu hao của cá được tính bởi hàm số:
$f\left( x \right)=300c\dfrac{{{\left( x+6 \right)}^{3}}}{x}=300c\left( {{x}^{2}}+18x+108+\dfrac{216}{x} \right)$ với $x{>}0$.
Ta có: ${f}’\left( x \right)=300c\left( 2x+18-\dfrac{216}{{{x}^{2}}} \right)=0\Leftrightarrow 2{{x}^{3}}+18{{x}^{2}}-216=0\Rightarrow x=3$.
Bảng biến thiên:
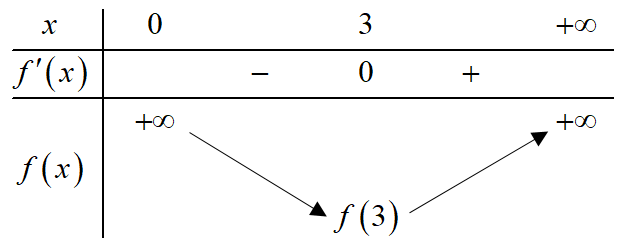
Vậy $\min\limits_{x\in \left( 0;+\infty \right)} f\left( x \right)=f\left( 3 \right)$ hay khi vận tốc của cá khi nước đứng yên là $v=9km/h$ thì cá ít tốn năng lượng nhất.
