Giả sử doanh số (tính bằng số sản phẩm) của một sản phẩm mới (trong vòng một số năm nhất định) tuân theo quy luật logistic được mô hình hoá bằng hàm số $f\left( t \right)=\dfrac{5000}{1+5{{e}^{-t}}},t\ge 0$ trong đó thời gian ${t }$ được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm ${f}’\left( t \right)$ sẽ biểu thị tốc độ bán hàng. Hỏi sau khi phát hành thì tốc độ bán hàng đạt lớn nhất bằng bao nhiêu?
Lời giải
Đáp án: $1250$.
Ta có $f\left( t \right)=\dfrac{5000}{1+5{{e}^{-t}}}=\dfrac{5000{{e}^{t}}}{{{e}^{t}}+5}$
$\Rightarrow {f}’\left( t \right)=\dfrac{5000{{e}^{t}}\left( {{e}^{t}}+5 \right)-5000{{e}^{2t}}}{{{\left( {{e}^{t}}+5 \right)}^{2}}}=\dfrac{25000.{{e}^{t}}}{{{\left( {{e}^{t}}+5 \right)}^{2}}}{>}0,\forall t\ge 0$
$\Rightarrow {f}”\left( t \right)=\dfrac{25000.{{e}^{t}}.{{\left( {{e}^{t}}+5 \right)}^{2}}-50000.{{e}^{t}}.\left( {{e}^{t}}+5 \right).{{e}^{t}}}{{{\left( {{e}^{t}}+5 \right)}^{4}}}$
$=\dfrac{25000.{{e}^{t}}.\left( {{e}^{t}}+5 \right).\left( {{e}^{t}}+5-2{{e}^{t}} \right)}{{{\left( {{e}^{t}}+5 \right)}^{4}}}$ $=\dfrac{25000.{{e}^{t}}.\left( 5-{{e}^{t}} \right)}{{{\left( {{e}^{t}}+5 \right)}^{3}}}$
$$ Có ${f}”\left( t \right)=0\Leftrightarrow 5-{{e}^{t}}=0\Leftrightarrow t=\ln 5.$
Ta có bảng biến thiên
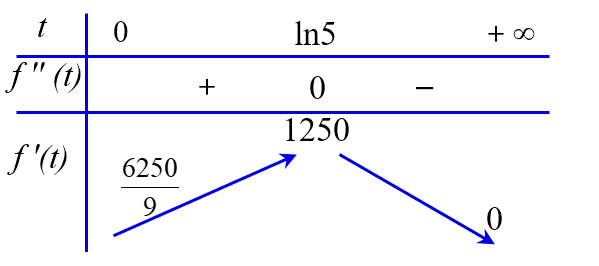
Dựa vào bảng biến thiên ta có tốc độ bán hàng lớn nhất là $1250$.
