Giả sử tỷ lệ sinh của Tỉnh $A$ tuân theo quy luật logistic được mô hình hóa bằng hàm số $f\left( t \right)=\dfrac{200}{1+4{{e}^{-t}}};t\ge 0,t\in N$, trong đó thời gian $t$ được tính bằng tháng. Khi đó đạo hàm $f’\left( t \right)$ sẽ biểu thị tốc độ tăng dân số của tỉnh $A$. Hỏi sau bao nhiêu tháng tốc độ tăng trưởng của dân số tỉnh $A$ là lớn nhất?
Lời giải
Đáp án: $1,39$.
Ta có $f\left( t \right)=\dfrac{200}{1+4{{e}^{-t}}}=\dfrac{200{{e}^{t}}}{{{e}^{t}}+4}$
Khi đó $f’\left( t \right)=\dfrac{800{{e}^{t}}}{{{\left( {{e}^{t}}+4 \right)}^{2}}}$
$\Rightarrow f”\left( t \right)=\dfrac{800{{e}^{t}}\left( 4-{{e}^{t}} \right)}{{{\left( {{e}^{t}}+4 \right)}^{3}}}$. Khi đó $f”\left( t \right)=0\Leftrightarrow t=\ln 4$.
Dựa vào bảng biến thiên
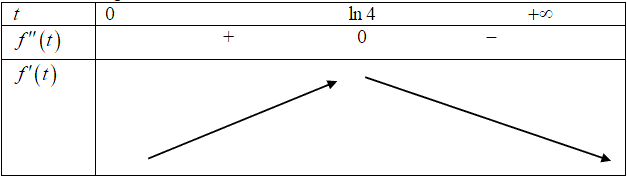
Vậy tốc độ tăng trưởng của dân số tỉnh $A$ lớn nhất là ${f}’\left( \ln 4 \right)=\dfrac{800{{e}^{\ln 4}}}{{{\left( {{e}^{\ln 4}}+4 \right)}^{2}}}=\dfrac{800.4}{{{16}^{2}}}=\dfrac{25}{2}$ tại thời điểm $t=\ln 4\approx 1,39$
