Một máy bay trình diễn có đường bay gắn với hệ trục $Oxy$ được mô phỏng như hình vẽ, trục $Ox$ gắn với mặt đất.
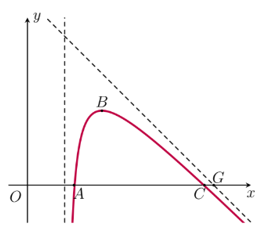
Đường bay có dạng là một phần của đồ thị hàm phân thức bậc hai trên bậc nhất $y=f\left( x \right)$ có đường tiệm cận đứng là $x=2$. Điểm $G$ là giao điểm của đường tiệm cận xiên của đồ thị hàm số $y=f\left( x \right)$ và trục $Ox$ được gọi là điểm giới hạn. Biết máy bay bay từ vị trí $A$ cách tọa tọa độ $O$ một khoảng $2,5$ đơn vị và máy bay khi ở vị trí cao nhất cách điểm xuất phát $1,5$ đơn vị theo phương song song với trục $Ox$ và cách mặt đất $4,5$ đơn vị. Vị trí máy bay tiếp đất cách điểm giới hạn một khoảng bằng bao nhiêu?
Lời giải
Đáp án: $0,5$.
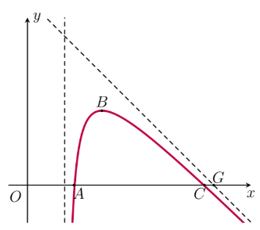
Vì tiệm cận đứng của đồ thị hàm số $y=f\left( x \right)$ (hàm phân thức bậc hai trên bậc nhất) là $x=2$.
Hàm số có dạng $y=f\left( x \right)=ax+b+\dfrac{c}{x-2}\left( a{<}0 \right)$.
Đồ thị hàm số qua điểm $A\left( \dfrac{5}{2};0 \right)$ và nhận $B\left( 4;\dfrac{9}{2} \right)$ làm điểm cực trị, suy ra:
$\left\{ \begin{array}{l}
f\left( \dfrac{5}{2} \right)=0 \\
f\left( 4 \right)=\dfrac{9}{2} \\
{f}’\left( 4 \right)=0 \\
\end{array} \right.\Rightarrow \left\{ \begin{array}{l}
\dfrac{5}{2}a+b+2c=0 \\
4a+b+\dfrac{1}{2}c=\dfrac{9}{2} \\
a-\dfrac{1}{4}c=0 \\
\end{array} \right.\Leftrightarrow \left\{ \begin{array}{l}
a=-1 \\
b=\dfrac{21}{2} \\
c=-4 \\
\end{array} \right.$. Khi đó: $f\left( x \right)=-x+\dfrac{21}{2}-\dfrac{4}{x-2}$.
Đồ thị hàm số có tiệm cận xiên: $y=-x+\dfrac{21}{2}$. Tọa độ điểm $G\left( \dfrac{21}{2};0 \right)$.
Phương trình cho hoành độ giao điểm của đồ thị hàm số $y=f\left( x \right)$ với trục $Ox$ là
$-x+\dfrac{21}{2}-\dfrac{4}{x-2}=0\Rightarrow -{{x}^{2}}+\dfrac{25}{2}x-25=0\Leftrightarrow \left[ \begin{array}{l}
x=\dfrac{5}{2} \\
x=10 \\
\end{array} \right.$ $\Rightarrow C\left( 10;0 \right)$.
$CG=\dfrac{21}{2}-10=\dfrac{1}{2}$.
