Trong hệ trục tọa độ $\left( Oxy \right)$ cho đồ thị hàm số $\left( C \right):y=\dfrac{{{x}^{2}}+x+1}{x+1}$ mô tả chuyển động của hai tàu đánh cá $A$ và $B$ (đơn vị trên mỗi trục tọa độ tính bằng $km$ ).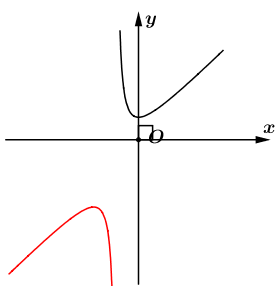 
Biết quỹ đạo chuyển động của hai tàu luôn thuộc về hai nhánh khác nhau của đồ thị $\left( C \right)$. Tính khoảng cách ngắn nhất (đơn vị $km$ ) giữa hai tàu đánh cá $A$ và $B$ (kết quả làm tròn đến hàng phần trăm).
Lời giải
Đáp án: $4,39$.
Ta có $y=\dfrac{{{x}^{2}}+x+1}{x+1}$ $=x+\dfrac{1}{x+1}$, $\left( x\ne -1 \right)$
Đồ thị hàm số có đường tiệm cận đứng $x=-1$, gồm hai nhánh nằm về hai phía của đường thẳng $x=-1$.
Gọi $A$ là điểm thuộc nhánh trái của đồ thị hàm số, khi đó ${{x}_{A}}{<}-1$.
Đặt $a=-1-{{x}_{A}}{>}0\Rightarrow {{x}_{A}}=-1-a$
$\Rightarrow {{y}_{A}}=-1-a+\dfrac{1}{-1-a+1}=-1-a-\dfrac{1}{a}$ $\Rightarrow A\left( -1-a;-1-a-\dfrac{1}{a} \right)$
Gọi $B$ là điểm thuộc nhánh phải của đồ thị hàm số, khi đó ${{x}_{B}}{>}-1$.
Đặt $b={{x}_{B}}+1{>}0$ $\Rightarrow {{x}_{B}}=b-1$
$\Rightarrow {{y}_{B}}=b-1+\dfrac{1}{b-1+1}=b-1+\dfrac{1}{b}$ $\Rightarrow B\left( b-1;b-1+\dfrac{1}{b} \right)$
$\Rightarrow A{{B}^{2}}={{\left( b+a \right)}^{2}}+{{\left( \dfrac{1}{b}+\dfrac{1}{a} \right)}^{2}}={{\left( b+a \right)}^{2}}+{{\left( b+a \right)}^{2}}.{{\left( \dfrac{1}{ab} \right)}^{2}}$ $={{(a+b)}^{2}}\left( 2+\dfrac{2}{ab}+\dfrac{1}{{{a}^{2}}{{b}^{2}}} \right)$
Với $a{>}0,b{>}0$ ta có $\left\{ \begin{array}{l}
{{\left( a+b \right)}^{2}}\ge 4ab \\
2+\dfrac{1}{{{a}^{2}}{{b}^{2}}}\ge 2\sqrt{\dfrac{2}{{{a}^{2}}{{b}^{2}}}}=\dfrac{2\sqrt{2}}{ab} \\
\end{array} \right.$
Nên $A{{B}^{2}}\ge 4ab.\left( \dfrac{2}{ab}+\dfrac{2\sqrt{2}}{ab} \right)=8+8\sqrt{2}\Rightarrow AB\ge \sqrt{8+8\sqrt{2}}\approx 4,39$.
Dấu bằng xảy $\text{ra}\Leftrightarrow \left\{ \begin{array}{*{35}{l}}
a=b \\
2=\dfrac{1}{{{a}^{2}}{{b}^{2}}} \\
\end{array}\Leftrightarrow a=b=\dfrac{1}{\sqrt[4]{2}} \right.$.
Vậy khoảng cách ngắn nhất (đơn vị $km$ ) giữa hai tàu đánh cá $A$ và $B$ là 4,39 (km).