Bài toán: Có hai hộp bóng $A$ và $B$ chỉ đựng các quả bóng đỏ và trắng, trong đó hộp $B$ đựng 4 quả bóng đỏ và 5 quả bóng trắng; tổng số bóng hai hộp không qua 20. Xét hai phép thử ngẫu nhiên sau:
Phép thử thứ nhất: Lấy ngẫu nhiên 1 quả bóng từ hộp $A$ bỏ vào hộp $B$ rồi lấy ngẫu nhiên 1 quả bóng từ hộp B . Bằng thực nghiệm người ta biết được rằng khả năng lấy được quả bóng đỏ từ hộp thứ hai bằng $\dfrac{33}{70}$.
Phép thử thứ hai: Lấy ngẫu nhiên 2 quả bóng từ hộp $A$ bỏ vào hộp $B$. Sau đó tiếp tục lấy ngẫu nhiên 2 quả bóng từ hộp B .
a) Trong phép thử thứ nhất, nếu lấy được quả bóng đỏ từ hộp A bỏ sang hộp B thì xác suất lấy được quả bóng trắng từ hộp B bằng 0,4 .
b) Hộp thứ nhất đựng 4 quả bóng đỏ và 3 quả bóng trắng.
c) Xác suất để lấy được 2 quả bóng đỏ từ hộp B bằng $\dfrac{166}{1155}$.
d) Nếu biết rằng hai quả bóng lấy được từ hộp B cùng có màu đỏ, xác suất để có ít nhất 1 quả là từ hộp A chuyển sang bằng $\dfrac{67}{128}$.
Lời giải:
a) Mệnh đề sai.
Trong phép thử thứ nhất, nếu lấy được quả bóng đỏ từ hộp A bỏ sang hộp B thì khi đó hộp B có 5 quả bóng đỏ, 5 quả bóng trắng. Do đó xác suất lấy được quả bóng trắng từ hộp B bằng 0,5 .
b) Mệnh đề sai.
Trong phép thử thứ nhất, gọi các biến cố $X$ : “Lấy được quả bóng đỏ từ hộp A ” và $Y$ : “Lấy được quả bóng đỏ từ hộp thứ hai”. Đặt $P\left(X\right)=x\in \left(0;1\right)$; suy ra .
Ta có sơ đồ hình cây sau đây:
Theo giả thiết ta có $P\left(Y\right)=0,5x+0,6\left(1-x\right)=\dfrac{33}{70}\Rightarrow x=\dfrac{5}{7}$.
Vì tổng số bóng hai hộp bóng không quá 20 mà hộp B có 9 quả bóng nên hộp A có không quá 11 quả bóng, mà xác suất để lấy được quả bóng đỏ bằng $\dfrac{5}{7}$ nên hộp A có 5 quả bóng đỏ và 2 quả bóng trắng.
c) Mệnh đề sai.
Trong phép thử thứ hai, ta gọi 2 Đ là biến cố “Lấy đúng 2 quả bóng đỏ từ hộp B “.
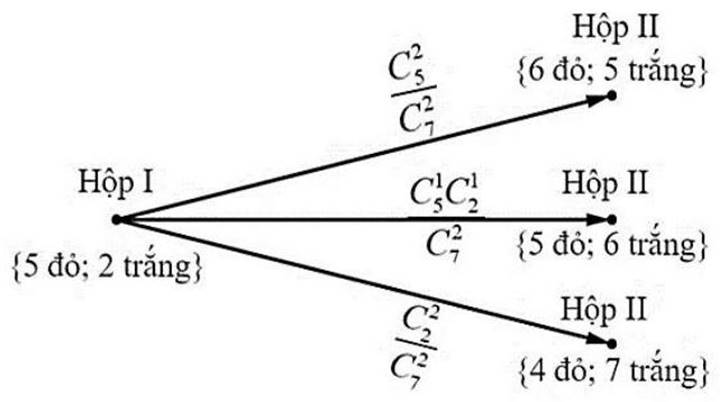
Với thông tin có được, ta có sơ đồ hình cây cho phép thử ngẫu nhiên thứ hai:
Từ đó suy ra .

d) Mệnh đề sai.
Gọi $X$ là biến cố lấy được ít nhất 1 quả là từ hộp A chuyển sang, ta có:

