Bài toán: Song sinh có thể là cùng trứng (identical) hoặc khác trứng (fraternal). Biết rằng $1/3$ số cặp song sinh là cùng trứng. Hiển nhiên, song sinh cùng trứng phải cùng giới tính; song sinh khác trứng có thể cùng hoặc khác giới tính. Giả sử song sinh cùng trứng có xác suất là hai bé trai hoặc hai bé gái như nhau, trong khi với song sinh khác trứng thì tất cả bốn khả năng đều có xác suất như nhau. Một nhà khảo sát tìm gặp ngẫu nhiên một người phụ nữ đang mang thai đôi.
a) Xác suất để người phụ nữ mang thai đôi là bé gái bằng 0,5 biết rằng đây là cặp song sinh cùng trứng.
b) Xác suất để thai đôi của người phụ nữ là một cặp trai gái bằng 0,3
c) Xác suất để thai đôi không cùng trứng và cũng không phải con trai bằng $\dfrac{1}{3}$.
d) Xác suất để người phụ nữ mang thai đôi là cùng trứng bằng 0,5 biết rằng cô ấy hạ sinh được hai bé gái.
Lời giải:
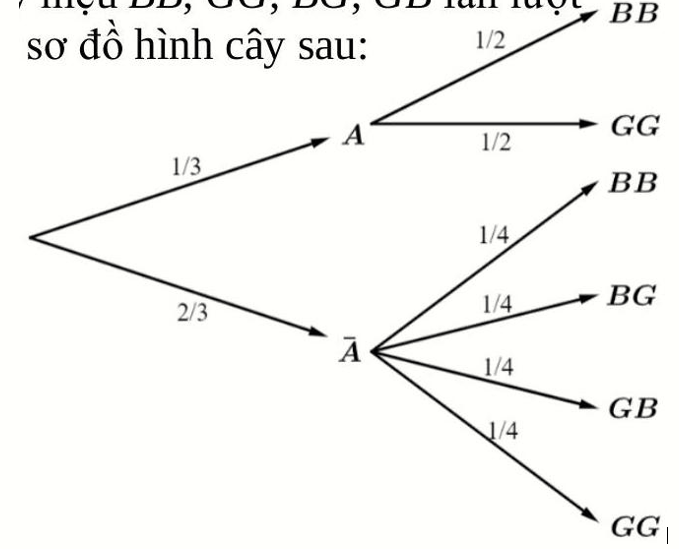
Gọi $A$ là biến cố: “Người phụ nữ mang thai đôi cùng trứng”, cá ký hiệu $BB,GG,BG,GB$ lần lượt chỉ các biến cố thai đôi là trai-trai, gái-gái, trai-gái, gái trai. Ta có sơ đồ hình cây sau:
a) Mệnh đề đúng.
Ta có $P\left(GG\mid A\right)=\dfrac{1}{2}$.
b) Mệnh đề sai.
Ta có .
c) Mệnh đề sai.
Ta có .

d) Mệnh đề đúng. Ta có $P\left(GG\right)=\dfrac{1}{3}\cdot \dfrac{1}{2}+\dfrac{2}{3}\cdot \dfrac{1}{4}=\dfrac{1}{3}$.
Do đó $P\left(A\mid GG\right)=\dfrac{P\left(A\right)\cdot P\left(GG\mid A\right)}{P\left(GG\right)}=\dfrac{\dfrac{1}{3}\cdot \dfrac{1}{2}}{\dfrac{1}{3}}=0,5$.
