Giải bài 5 Trường hợp bằng nhau thứ hai của tam giác cạnh – góc – cạnh – Chương 7 Toán 7 Cánh diều
============
Câu hỏi khởi động trang 84 SGK Toán 7 Cánh diều tập 2 – CD
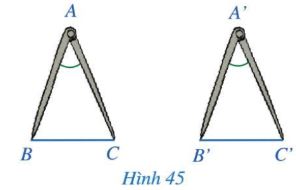
Hai chiếc compa ở Hình 45 gợi nên hình ảnh hai tam giác ABC và A’B’C’ có: AB = A’B’, AC = A’C’, \(\widehat A = \widehat {A’}\).

Hai tam giác ABC và A’B’C’ có bằng nhau hay không?
Phương pháp giải
Học sinh có thể dùng thước để đo độ dài cạnh BC và B’C’ rồi so sánh.
Lời giải chi tiết
Hai tam giác ABC và A’B’C’ có bằng nhau.
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 5
Hoạt động 1 trang 84 SGK Toán 7 Cánh diều tập 2 – CD
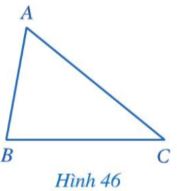
Cho tam giác ABC (Hình 46). Nêu hai cạnh của góc tại đỉnh A.
Phương pháp giải
Quan sát hình và trả lời câu hỏi
Lời giải chi tiết
Hai cạnh của góc tại đỉnh A là cạnh AB và cạnh AC.
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 5
Hoạt động 2 trang 84 SGK Toán 7 Cánh diều tập 2 – CD
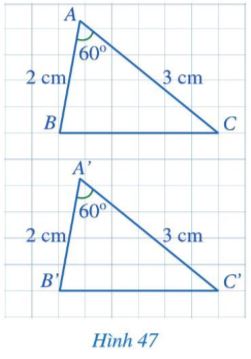
Cho hai tam giác ABC và A’B’C’ (Hình 47) có: AB = A’B’ = 2 cm, \(\widehat A = \widehat {A’} = 60^\circ \), AC = A’C’ = 3 cm. Bằng cách đếm số ô vuông, hãy so sánh BC và B’C’. Từ đó có thể kết luận được hai tam giác ABC và A’B’C’ bằng nhau hay không?
Phương pháp giải
Đếm số ô vuông rồi so sánh BC và B’C’. Từ đó so sánh hai tam giác ABC và A’B’C’.
Lời giải chi tiết
BC = B’C’ = 6 (ô vuông).
Tam giác ABC và A’B’C’ có các cặp cạnh tương ứng bằng nhau nên tam giác ABC bằng tam giác A’B’C’ (c.c.c)
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 5
Luyện tập 1 trang 85 SGK Toán 7 Cánh diều tập 2 – CD
Cho góc nhọn xOy. Hai điểm M, N thuộc tia Ox thỏa mãn OM = 2 cm, ON = 3 cm. Hai điểm P, Q thuộc tia Oy thỏa mãn OP = 2 cm, OQ = 3 cm. Chứng minh MQ = NP.
Phương pháp giải
Chứng minh tam giác OMQ bằng tam giác OPN. Hai tam giác bằng nhau thì các cặp cạnh tương ứng bằng nhau.
Lời giải chi tiết
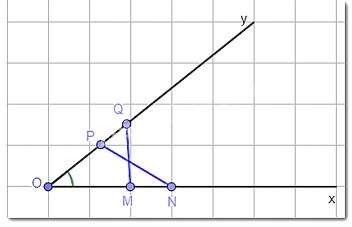
Xét tam giác OMQ và tam giác OPN có: OM = OP (= 2 cm); OQ = ON (= 3 cm); góc O chung.
Vậy \(\Delta OMQ = \Delta OPN\) (c.g.c)
\(\Rightarrow MQ = NP\) ( 2 cạnh tương ứng)
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 5
Luyện tập 2 trang 85 SGK Toán 7 Cánh diều tập 2 – CD
Cho góc xOy có Oz là tia phân giác. Hai điểm M, N lần lượt thuộc Ox, Oy và khác O thỏa mãn OM = ON, điểm P khác O và thuộc Oz. Chứng minh MP = NP.
Phương pháp giải
Muốn chứng minh MP = NP, ta chứng minh tam giác MOP bằng tam giác NOP.
Lời giải chi tiết
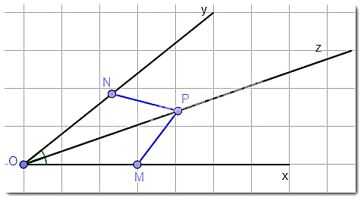
Xét tam giác MOP và tam giác NOP có: OM = ON, OP chung, \(\widehat {MOP} = \widehat {NOP}\)(vì Oz là tia phân giác).
Vậy \(\Delta MOP = \Delta NOP\)(c.g.c)
\(\Rightarrow MP = NP\) ( 2 cạnh tương ứng)
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 5
Giải bài 1 trang 86 SGK Toán 7 Cánh diều tập 2 – CD
Chứng minh định lí: “Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn” (trang 74) thông qua việc giải bài tập sua đây:
Cho tam giác ABC có AB < AC. Tia phân giác của góc BAC cắt cạnh BC tại D. Điểm E thuộc cạnh AC thỏa mãn AE = AB. Chứng minh:
a) \(\Delta ABD = \Delta AED\);
b) \(\widehat B > \widehat C\).
Phương pháp giải
a) Chứng minh hai tam giác bằng nhau theo trường hợp c.g.c.
b) Chứng minh \(\widehat B > \widehat C\) dựa vào kết quả phần a và tổng ba góc trong một tam giác bằng 180°.
Lời giải chi tiết
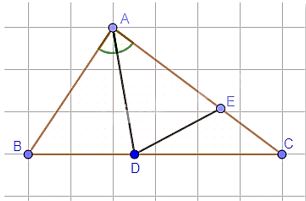
a) Xét hai tam giác ABD và AED: AB = AE, AD chung, \(\widehat {BAD} = \widehat {EAD}\)(AD là phân giác của góc BAC).
Vậy \(\Delta ABD = \Delta AED\) (c.g.c)
b) Ta có: \(\Delta ABD = \Delta AED \Rightarrow \widehat {ABD} = \widehat {AED}\) (2 góc tương ứng)
Ba điểm A, E, C thẳng hàng nên \(\widehat {AED} = 180^\circ \).
Vậy \(\widehat {ABD} = \widehat {AED} = 180^\circ – \widehat {DEC} = \widehat {EDC} + \widehat {ECD}\)(Tổng ba góc trong tam giác EDC bằng 180°).
Do đó, góc B bằng tổng của góc EDC và góc C. Vậy \(\widehat B > \widehat C\).
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 5
Giải bài 2 trang 86 SGK Toán 7 Cánh diều tập 2 – CD
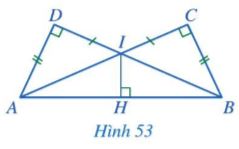
Cho Hình 53 có AD = BC, IC = ID, các góc tại đỉnh C, D, H là góc vuông. Chứng minh:
a) IA = IB;
b) IH là tia phân giác của góc AIB.
Phương pháp giải
a) Chứng minh IA = IB, ta chứng minh tam giác IDA bằng tam giác ICB.
b) Một đường thẳng là đường vuông góc hạ từ một đỉnh của tam giác cân tại đỉnh đó thì đường thẳng đó là tia phân giác của tam giác đó.
Lời giải chi tiết
a) Xét tam giác IDA và tam giác ICB có: ID = IC, DA = CB, \(\widehat D = \widehat C = 90^\circ \).
Vậy \(\Delta IDA = \Delta ICB\) (c.g.c)
\(\Rightarrow IA = IB\) (2 cạnh tương ứng)
b) Xét tam giác vuông IHA và tam giác vuông IHB có: IH chung; IA = IB
Vậy \(\Delta IHA = \Delta IHB\) (cạnh huyền – cạnh góc vuông)
\(\Rightarrow \widehat{AIH}=\widehat{BIH}\) ( 2 góc tương ứng)
Mà tia IH nằm trong góc AIB
\(\Rightarrow \) IH là tia phân giác của góc AIB.
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 5
Giải bài 3 trang 86 SGK Toán 7 Cánh diều tập 2 – CD
Có hai xã cùng ở một bên bờ sông Lam. Các kĩ sư muốn bắc một cây cầu qua sông Lam cho người dân hai xã. Để thuận lợi cho người dân đi lại, các kĩ sư cần phải chọn vị trí của cây cầu sao cho tổng khoảng cách từ hai xã đến chân cầu là nhỏ nhất. Bạn Nam đề xuất cách xác định vị trí của cây cầu như sau (Hình 54):
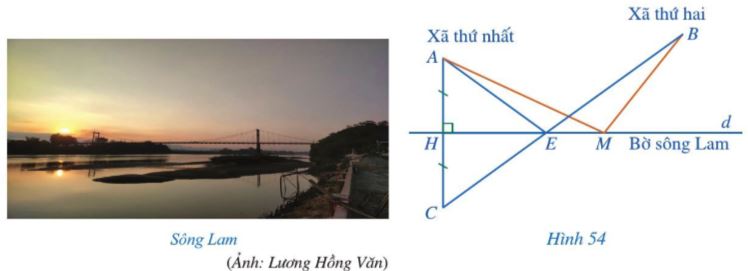
– Kí hiệu điểm A chỉ vị trí xã thứ nhất, điểm B chỉ vị trí xã thứ hai, đường thẳng d chỉ vị trí bờ sông Lam.
– Kẻ AH vuông góc với d (H thuộc d), kéo dài AH về phía H và lấy C sao cho AH = HC.
– Nối C với B, CB cắt đường thẳng d tại E.
Khi đó, E là vị trí của cây cầu.
Bạn Nam nói rằng: Lấy một điểm M trên đường thẳng d, M khác E thì
MA + MB > EA + EB
Em hãy cho biết bạn Nam nói đúng hay sai. Vì sao?
Phương pháp giải
Muốn biết bạn Nam nói đúng hay không, ta chứng minh bất đẳng thức MA + MB > EA + EB là đúng hay sai.
Dựa vào:
– Tính chất đường trung trực.
– Trong một tam giác, tổng của hai cạnh luôn lớn hơn độ dài cạnh còn lại.
Lời giải chi tiết
Ta có: HA = HC, \(EH \bot AC\). Vậy EH là đường trung trực của AC nên EA = EC (tính chất đường trung trực của đoạn thẳng).
Tương tự ta có: MH là đường trung trực của AC nên MA = MC.
Xét tam giác MBC: \(BC < MB + MC\)(Trong một tam giác, tổng của hai cạnh luôn lớn hơn độ dài cạnh còn lại).
Ta có:
\(BC < MB + MC = MB + MA\). (1)
Ba điểm B, E, C thẳng hàng nên \(EB + EC = BC\). (2)
Thay (2) vào (1) ta được: \(\begin{array}{l}BC < MB + MA\\EB + EC < MA + MB\end{array}\)
Mà EA = EC nên \(EA + EB < MA + MB\). Vậy bạn Nam nói đúng và khi đó để tổng khoảng cách từ hai xã đến chân cầu là nhỏ nhất thì E là vị trí của cây cầu
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 5
Giải bài 4 trang 87 SGK Toán 7 Cánh diều tập 2 – CD
Cho \(\Delta ABC = \Delta MNP\). Gọi D, E lần lượt là trung điểm của BC và CA; Q, R lần lượt là trung điểm của NP và PM. Chứng minh:
a) AD = MQ;
b) DE = QR.
Phương pháp giải
a) Chứng minh tam giác ABD bằng tam giác MNQ.
b) Chứng minh tam giác DEC bằng tam giác QRP.
Lời giải chi tiết
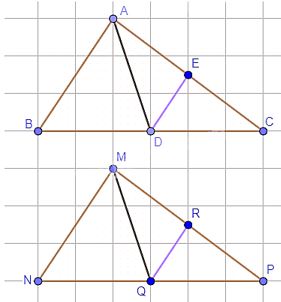
a) Xét hai tam giác ABD và tam giác MNQ:
AB = MQ (do \(\Delta ABC = \Delta MNP\)).
\(\widehat {ABD} = \widehat {MNQ}\) (\(\widehat {ABD} = \widehat {MNQ}\)).
BD = NQ (\(\dfrac{1}{2}BC = \dfrac{1}{2}NP\))
BC = NP (do \(\Delta ABC = \Delta MNP\)).
Vậy \(\Delta ABD = \Delta MNQ\)(c.g.c) nên AD = MQ ( 2 cạnh tương ứng)
b) Vì \(\Delta ABC = \Delta MNP\) nên BC = NP ( 2 cạnh tương ứng) . Do đó, \(\dfrac{1}{2}BC = \dfrac{1}{2}NP\) hay DC = QP
Vì \(\Delta ABC = \Delta MNP\) nên AC = MP ( 2 cạnh tương ứng) . Do đó, \(\dfrac{1}{2}AC = \dfrac{1}{2}MP\) hay EC = RP
Xét hai tam giác DEC và tam giác QRP:
DC = QP
\(\widehat {ECD} = \widehat {RPQ}\)(\(\Delta ABC = \Delta MNP\))
EC = RP
Vậy \(\Delta DEC = \Delta QRP\)(c.g.c) nên DE = QR ( 2 cạnh tương ứng)
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 5
