Giải bài 2 Quan hệ giữa góc và cạnh đối diện, bất đẳng thức tam giác – Chương 7 Toán 7 Cánh diều
============
Câu hỏi khởi động trang 74 SGK Toán 7 Cánh diều tập 2 – CD
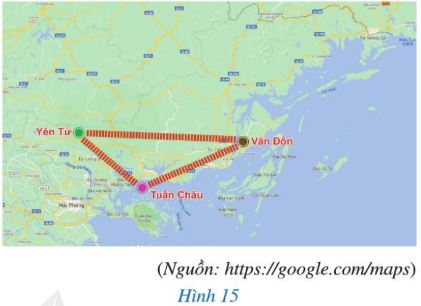
Hình 15 minh họa vị trí của ba khu du lịch Yên Tử, Tuần Châu và Vân Đồn (ở tỉnh Quảng Ninh).

Trong hai vị trí Yên Tử và Tuần Châu, vị trí nào gần Vân Đồn hơn?
Phương pháp giải
Học sinh có thể lấy thước kẻ (có kẻ vạch đo) để đo khoảng cách từ Yên Tử đến Vân Đồn và từ Tuần Châu đến Vân Đồn rồi so sánh.
Lời giải chi tiết
Trong hai vị trí Yên Tử và Tuần Châu thì Tuần Châu gần Vân Đồn hơn.
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 2
Hoạt động 1 trang 74 SGK Toán 7 Cánh diều tập 2 – CD
Quan sát tam giác ABC ở Hình 17.
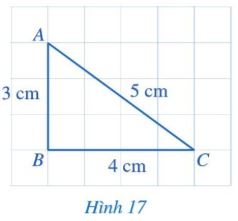
a) So sánh hai cạnh AB và AC.
b) So sánh góc B (đối diện với cạnh AC) và góc C (đối diện với cạnh AB).
Phương pháp giải
a) Dựa vào độ dài cạnh đã cho để so sánh hai cạnh AB và AC.
b) Tam giác ABC là tam giác có một góc vuông nên hai góc còn lại sẽ nhỏ hơn 90°.
Lời giải chi tiết
a) Trong tam giác ABC:
\(AB = 3\) cm, \(AC = 5\) cm.
Vậy AB < AC.
b) Trong tam giác ABC có \(\widehat B = 90^\circ \)mà tổng ba góc trong một tam giác bằng 180°.
\(\Rightarrow\) Góc C < 90°. Hay \(\widehat B > \widehat C\).
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 2
Luyện tập 1 trang 74 SGK Toán 7 Cánh diều tập 2 – CD
Cho tam giác MNP có \(MN = 4\)cm, \(NP = 5\)cm, \(MP = 6\) cm. Tìm góc nhỏ nhất, góc lớn nhất của tam giác MNP.
Phương pháp giải
Góc lớn nhất trong tam giác là góc đối diện với cạnh lớn nhất trong tam giác.
Góc nhỏ nhất trong tam giác là góc đối diện với cạnh nhỏ nhất trong tam giác.
Lời giải chi tiết
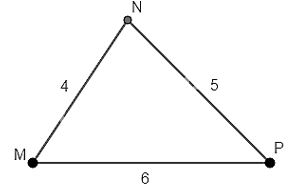
Trong tam giác MNP: \(MN < NP < MP\).
\(\Rightarrow\) Cạnh MN nhỏ nhất, MP lớn nhất trong tam giác MNP.
Vậy góc nhỏ nhất của tam giác MNP là góc P (đối diện với cạnh MN), góc lớn nhất của tam giác MNP là góc N (đối diện với cạnh MP)
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 2
Hoạt động 2 trang 75 SGK Toán 7 Cánh diều tập 2 – CD
Quan sát tam giác ABC ở Hình 19.
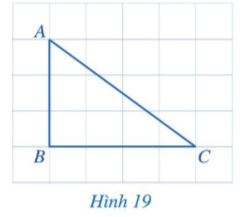
a) So sánh hai góc B và C.
b) So sánh cạnh AB (đối diện với góc C) và cạnh AC (đối diện với góc B).
Phương pháp giải
a) Tam giác ABC là tam giác có một góc vuông nên hai góc còn lại sẽ nhỏ hơn 90°.
b) Học sinh có thể dùng thước kẻ (có chia vạch đo) để so sánh hai cạnh hoặc dựa vào độ dài được kẻ của các cạnh trên hình (mỗi một cạnh ô vuông là 1 cm).
Lời giải chi tiết
a) Trong tam giác ABC có \(\widehat B = 90^\circ \)mà tổng ba góc trong một tam giác bằng 180°.
\(\Rightarrow\) Góc C < 90°. Hay \(\widehat B > \widehat C\).
b) Ta có: \(AB = 3\)cm, \(AC = 5\) cm. Vậy AB < AC.
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 2
Luyện tập 2 trang 75 SGK Toán 7 Cánh diều tập 2 – CD
a) Cho tam giác DEG có góc E là góc tù. So sánh DE và DG.
b) Cho tam giác MNP có \(\widehat M = 56^\circ \), \(\widehat N = 65^\circ \). Tìm cạnh nhỏ nhất, cạnh lớn nhất của tam giác MNP.
Phương pháp giải
a) So sánh hai góc đối diện với hai cạnh để so sánh hai cạnh. (Góc đối diện với cạnh lớn hơn thì cạnh lớn hơn)
b) Cạnh nhỏ nhất trong tam giác là cạnh đối diện với góc nhỏ nhất trong tam giác.
Cạnh lớn nhất trong tam giác là cạnh đối diện với góc lớn nhất trong tam giác.
Lời giải chi tiết
a)
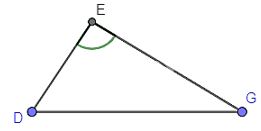
Trong tam giác DEG có góc E là góc tù (góc > 90°). Mà DG là cạnh đối diện với góc E nên DG là cạnh lớn nhất trong tam giác.
Vậy DE < DG.
b)
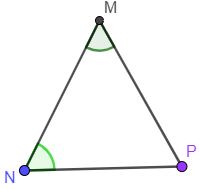
Tam giác MNP có \(\widehat M = 56^\circ \), \(\widehat N = 65^\circ \). Mà tổng ba góc trong một tam giác bằng 180°. Vậy \(\widehat P = 180^\circ – 56^\circ – 65^\circ = 59^\circ \).
Ta thấy: \(\widehat M < \widehat P < \widehat N\). Hay cạnh nhỏ nhất của tam giác MNP là NP (đối diện với góc M), cạnh lớn nhất của tam giác MNP là MP (đối diện với góc N).
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 2
Hoạt động 3 trang 75 SGK Toán 7 Cánh diều tập 2 – CD
Bạn An có hai con đường đi từ nhà đến trường. Đường đi thứ nhất là đường đi thẳng từ nhà đến trường, đường đi thứ hai là đường đi thẳng từ nhà đến hiệu sách rồi đi thẳng từ hiệu sách đến trường (Hình 20). Theo em, bạn An đi từ nhà đến trường theo đường nào sẽ gần hơn?
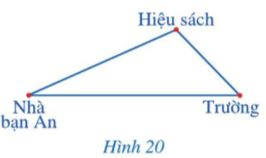
Phương pháp giải
Học sinh có thể lấy thước đo (có chia kẻ vạch) để đo hai quãng đường rồi so sánh.
Lời giải chi tiết
Bạn An đi đường đi thứ nhất là đường đi thẳng từ nhà đến trường sẽ gần hơn đường đi thứ hai là đường đi thẳng từ nhà đến hiệu sách rồi đi thẳng từ hiệu sách đến trường.
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 2
Hoạt động 4 trang 75 SGK Toán 7 Cánh diều tập 2 – CD
Bạn Thảo cho rằng tam giác ABC trong Hình 21 có \(AB = 3\)cm, \(BC = 2\)cm, \(AC = 4\)cm.
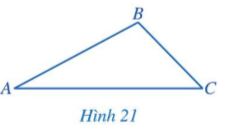
a) Hãy sử dụng thước thẳng (có chia đơn vị) để kiểm tra lại số đo độ dài ba cạnh của tam giác ABC mà bạn Thảo đã nói.
b) So sánh \(AB + BC\)và AC.
Phương pháp giải
a) Học sinh sử dụng thước thẳng (có chia đơn vị) để kiểm tra lại số đo độ dài ba cạnh của tam giác ABC.
b) Dựa vào độ dài của các cạnh để so sánh \(AB + BC\) và AC.
Lời giải chi tiết
a) Bạn Thảo nói đúng.
b) \(AB + BC = 3 + 2 = 5 > AC = 4\).
Vậy \(AB + BC\) > AC.
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 2
Luyện tập 3 trang 76 SGK Toán 7 Cánh diều tập 2 – CD
Cho tam giác ABC có \(AB = 2\)cm, \(BC = 4\)cm. So sánh hai cạnh AC và AB.
Phương pháp giải
Trong một tam giác, hiệu độ dài hai cạnh bất kì luôn nhỏ hơn độ dài cạnh còn lại.
Lời giải chi tiết
Ta có: \(BC – AC = 4 – 2 = 2\).
Vậy độ dài cạnh AC lớn hơn 2 hay AC > AB (vì\(AB = 2\)cm).
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 2
Giải bài 1 trang 76 SGK Toán 7 Cánh diều tập 2 – CD
Cho tam giác MNP có \(MN = 6\)cm, \(NP = 8\)cm, \(PM = 7\)cm. Tìm góc nhỏ nhất, góc lớn nhất của tam giác MNP.
Phương pháp giải
Góc lớn nhất (nhỏ nhất) trong tam giác là góc đối diện với cạnh lớn nhất (nhỏ nhất) trong tam giác đó.
Lời giải chi tiết
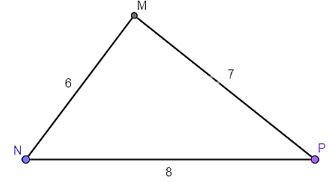
Trong tam giác MNP ta có: \(MN < MP < NP\) (6 < 7 < 8).
Vậy góc lớn nhất trong tam giác MNP là góc M (đối diện với cạnh NP) và góc nhỏ nhất trong tam giác MNP là góc P (đối diện với cạnh MN).
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 2
Giải bài 2 trang 76 SGK Toán 7 Cánh diều tập 2 – CD
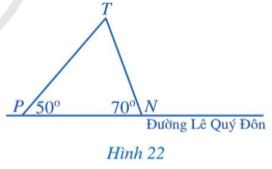
Bạn Hoa đi học từ nhà đến trường bằng cách đi xe buýt dọc theo đường Lê Quý Đôn và xuống xe tại một trong hai điểm dừng N hoặc P, rồi từ đó đi bộ đến trường T (Hình 22). Bạn Hoa nên xuống ở điểm dừng nào để quãng đường đi bộ đến trường ngắn hơn?
Phương pháp giải
Để biết bạn Hoa nên xuống ở điểm dừng nào, ta so sánh hai cạnh PT và NT với nhau bằng cách so sánh hai góc đối diện của chúng
Lời giải chi tiết
Ta thấy: \(\widehat P < \widehat N\)(50° < 70°).
Vậy PT (cạnh đối diện với góc N) > NT (cạnh đối diện với góc P). Hay bạn Hoa nên xuống ở điểm dừng P rồi đi bộ đến trường.
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 2
Giải bài 3 trang 76 SGK Toán 7 Cánh diều tập 2 – CD
Theo https://vietnamnet.vn ngày 01/10/2020, sóng 4G có thể phủ kín đến bán kính 100 km.
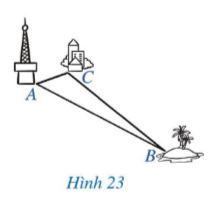
Người ta đặt một trạm phát sóng 4G tại vị trí A. Có một đảo nhỏ (tại vị trí B) chưa biết khoảng cách đến vị trí A nhưng lại biết khoảng cách từ đảo đó đến một khách sạn (tại vị trí C) là 75 km và khách sạn đó cách vị trí A là 20 km (Hình 23). Sóng 4G của trạm phát sóng A có thể phủ đến đảo đó được không? Vì sao?
Phương pháp giải
Muốn biết trạm phát sóng A có thể phủ sóng đến đảo B được hay không, ta so sánh độ dài cạnh AB với 100.
Tổng hai cạnh bất kì trong một tam giác luôn lớn hơn độ dài cạnh còn lại.
Lời giải chi tiết
Ta xét tam giác ABC: \(AC = 20\) km, \(BC = 75\) km.
Và \(AC + BC = 25 + 75 = 100\) km. Mà tổng hai cạnh bất kì trong một tam giác luôn lớn hơn độ dài cạnh còn lại.
Hay\(AC + BC = 100\) > AB. Vậy sóng 4G của trạm phát sóng A có thể phủ đến đảo B. (Vì sóng 4G có thể phủ kín đến bán kính 100 km).
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 2
Giải bài 4 trang 77 SGK Toán 7 Cánh diều tập 2 – CD
Bộ ba số đo độ dài nào trong mỗi trường hợp sau không thể là độ dài ba cạnh của một tam giác?
a) 8 cm, 5 cm, 3 cm;
b) 8 cm, 5 cm, 4 cm;
c) 8 cm, 5 cm, 2 cm.
Phương pháp giải
Hiệu hai cạnh bất kì trong một tam giác luôn nhỏ hơn cạnh còn lại trong tam giác đó.
Lời giải chi tiết
a) Ta thấy: \(\begin{array}{l}8 – 5 = 3 = 3\\8 – 3 = 5 = 5\end{array}\)
Vậy bộ ba số đo độ dài 8 cm, 5 cm, 3 cm không thể là độ dài ba cạnh của một tam giác.
b) Ta thấy: \(\begin{array}{l}8 – 5 = 3 < 4\\8 – 4 = 4 < 4\\5 – 4 = 1 < 8\end{array}\)
Vậy bộ ba số đo độ dài 8 cm, 5 cm, 4 cm có thể là độ dài ba cạnh của một tam giác.
c) Ta thấy: \(8 – 5 = 3 > 2\).
Vậy bộ ba số đo độ dài 8 cm, 5 cm, 2 cm không thể là độ dài ba cạnh của một tam giác.
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 2
Giải bài 5 trang 77 SGK Toán 7 Cánh diều tập 2 – CD
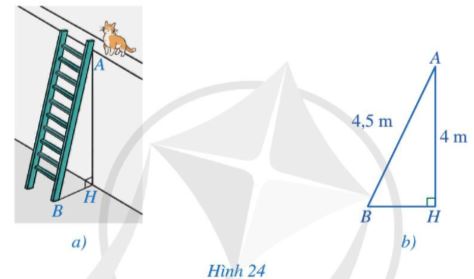
Con mèo của bạn Huê bị mắc kẹt trên gờ tường cao 4 m. Bác bảo vệ sử dụng một cái thang để đưa mèo xuống giúp bạn Huê. Bác đặt thang dựa vào gờ tường (Hình 24a), khoảng cách từ chân thang đến điểm chạm vào gờ tường là \(AB = 4,5\)m. Hình 24b mô tả hình ảnh chiếc thang dựa vào tường trong Hình 24a. Bạn Huê khẳng định chân thang cách chân tường là \(BH = 0,5\)m. Khẳng định của bạn Huê có đúng không? Vì sao?
Phương pháp giải
Muốn biết bạn Huê nói đúng hay không, ta so sánh độ dài cạnh BH với hiệu của hai cạnh còn lại trong tam giác là AB và AH.
Hiệu hai cạnh trong một tam giác luôn nhỏ hơn độ dài cạnh còn lại của tam giác đó
Lời giải chi tiết
Ta có: \(AH = 4\)m, \(AB = 4,5\)m.
\(AB – AH = 4,5 – 4 = 0,5\). Mà hiệu hai cạnh trong một tam giác luôn nhỏ hơn độ dài cạnh còn lại của tam giác đó nên 0,5 < BH.
Bạn Huê khẳng định chân thang cách chân tường là \(BH = 0,5\) m là sai.
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 2
Giải bài 6 trang 77 SGK Toán 7 Cánh diều tập 2 – CD
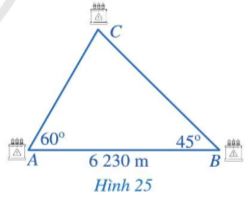
Người ta cần làm đường dây điện từ một trong hai trạm biến áp A, B đến trạm biến áp C trên đảo (Hình 25).
a) Đường dây điện xuất phát từ trạm biến áp nào đến trạm biến áp C sẽ ngắn hơn.
b) Bạn Bình ước lượng: Nếu làm cả hai đường dây điện từ A và B đến C thì tổng độ dài đường dây khoảng 6 200 m. Bạn Bình ước lượng có đúng không?
Phương pháp giải
a) Muốn biết đường dây xuất phát từ trạm biến áp nào đến C sẽ ngắn hơn ta so sánh hai cạnh AC và BC (bằng cách so sánh hai góc đối diện của chúng. Góc nào nhỏ hơn thì cạnh đối diện ngắn hơn).
b) Tổng độ dài của hai cạnh bất kì trong một tam giác luôn lớn hơn độ dài cạnh còn lại.
Lời giải chi tiết
a) Ta có: \(\widehat B = 45^\circ < \widehat A = 60^\circ \). Vậy AC (đối diện góc B) < BC (đối diện góc A) hay đường dây điện xuất phát từ trạm biến áp A đến trạm biến áp C sẽ ngắn hơn.
b) Ta có: \(AB + BC > AB = 6230\)m. Nên bạn Bình ước lượng: Nếu làm cả hai đường dây điện từ A và B đến C thì tổng độ dài đường dây khoảng 6 200 m là sai.
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 2
Giải bài 7 trang 77 SGK Toán 7 Cánh diều tập 2 – CD
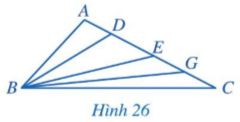
Cho tam giác ABC có góc A tù. Trên cạnh AC lần lượt lấy các điểm D, E, G sao cho D nằm giữa A và E; E nằm giữa D và G; G nằm giữa E và C (Hình 26). Sắp xếp các đoạn thẳng BA, BD, BE, BG, BC theo thứ tự tăng dần. Giải thích vì sao?
Phương pháp giải
Muốn sắp xếp được các đoạn thẳng theo thứ tự tăng dần, ta so sánh chúng với BA và cạnh còn lại trong tam giác tương ứng
Lời giải chi tiết
Xét tam giác BAD:
+ Góc A tù (góc > 90°) nên cạnh BD là cạnh lớn nhất trong tam giác này (đối diện với góc A).
Nên BD > BA.
+ Góc A tù nên góc ABD và góc ADB là góc nhọn → góc BDE là góc tù (ba điểm A, D, E thẳng hàng hay góc ADE =180°). Vậy BE (đối diện với góc BDE) > BD.
Tương tự, ta có:
+ Góc BDE là góc tù nên góc DBE và góc DEB là góc nhọn → góc BEG là góc tù. Vậy BG > BE.
+ Góc BEG là góc tù nên góc EBG và góc EGB là góc nhọn → góc BGC là góc tù. Vậy BC > BG.
Vậy BA < BD <BE < BG < BC.
Hay các đoạn thẳng BA, BD, BE, BG, BC theo thứ tự tăng dần là: BA, BD, BE, BG, BC.
Giải bài tập Toán 7 Cánh diều Chương 7 Bài 2
