Phương pháp : Các bước khảo sát và vẽ đồ thị hàm số trùng phương $y = a{x^4} + b{x^2} + c$ với $a ≠ 0.$
+ Bước 1. TXĐ: $D=\mathbb{R}.$
+ Bước 2. Đạo hàm: ${y}’=4a{{x}^{3}}+2bx$ $=2x(2a{{x}^{2}}+b)$ $\Rightarrow {y}’=0\Leftrightarrow x=0$ hoặc ${{x}^{2}}=-\frac{b}{2a}$.
Nếu $ab\ge 0$ thì $y$ có một cực trị ${{x}_{0}}=0.$
Nếu $ab<0$ thì $y$ có $3$ cực trị ${{x}_{0}}=0$, $\text{ }{{x}_{1,2}}=\pm \sqrt{-\frac{b}{2a}}.$
+ Bước 3. Đạo hàm cấp $2$: ${y}”=12a{{x}^{2}}+2b$, $\text{ }{y}”=0\Leftrightarrow {{x}^{2}}=-\frac{b}{6a}.$
Nếu $ab\ge 0$ thì đồ thị không có điểm uốn.
Nếu $ab<0$ thì đồ thị có $2$ điểm uốn.
+ Bước 4. Bảng biến thiên và đồ thị:
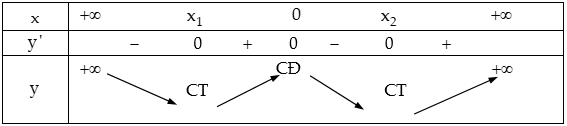
Trường hợp 1 . $a>0, b<0$: Hàm số có $3$ cực trị.

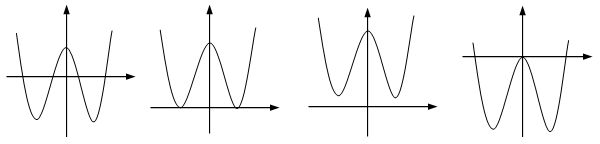
Trường hợp 2 . $a < 0, b > 0$: Hàm số có $3$ cực trị.
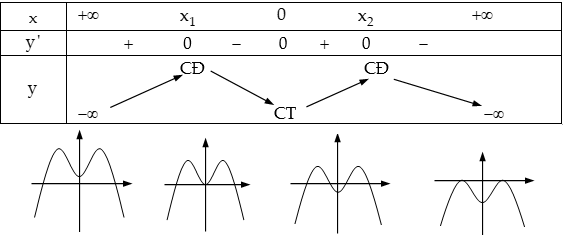
Trường hợp 3 . $a > 0,b \ge 0$: Hàm số có $1$ cực trị.
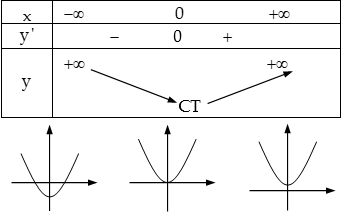
Trường hợp 4 . $a < 0, b \le 0$: Hàm số có $1$ cực trị.
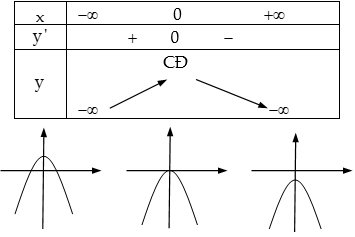
Một số tính chất của hàm số trùng phương :
+ Đồ thị của hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c\text{ }(a\ne 0)$ cắt trục hoành tại $4$ điểm phân biệt có hoành độ lập thành cấp số cộng khi phương trình: $a{{X}^{2}}+bX+c=0$ có $2$ nghiệm dương phân biệt thỏa ${{X}_{1}}=9{{X}_{2}}$.
+ Nếu đồ thị hàm số có ba điểm cực trị thì ba điểm cực trị tạo thành một tam giác cân có đỉnh nằm trên $Oy.$
+ Nếu đường thẳng $d$ là tiếp tuyến của đồ thị thì đường thẳng $d’$ đối xứng với $d$ qua $Ox$ cũng là tiếp tuyến của đồ thị.
Ví dụ minh họa :
Ví dụ 1 . Cho hàm số $y={{x}^{4}}-2{{x}^{2}}-1$ có đồ thị $(C).$
1. Khảo sát sự biến thiên và vẽ đồ thị $(C)$ của hàm số.
2. Dùng đồ thị $(C)$, hãy biện luận theo $m$ số nghiệm thực của phương trình ${{x}^{4}}-2{{x}^{2}}-1=m \left( * \right).$
1. Khảo sát sự biến thiên và vẽ đồ thị:
Tập xác định: $D=\mathbb{R}.$
Chiều biến thiên:
Ta có: $y’=4{{x}^{3}}-4x$ $= 4x\left( {{x}^{2}}-1 \right).$
$y’=0\Leftrightarrow 4x\left( {{x}^{2}}-1 \right)=0$ $\Leftrightarrow x=0$ hoặc $x=\pm 1.$
$y’ > 0 \Leftrightarrow x \in \left( { – 1;0} \right) \cup \left( {1; + \infty } \right)$, $y’ < 0 \Leftrightarrow x \in \left( { – \infty ; – 1} \right) \cup \left( {0;1} \right).$
Hàm số nghịch biến trên các khoảng $\left( { – \infty ; – 1} \right)$ và $\left( {0;1} \right)$, đồng biến trên các khoảng $\left( -1;0 \right)$ và $\left( 1;+\infty \right)$.
Hàm số đạt cực đại tại điểm $x=0$; giá trị cực đại của hàm số là $y\left( 0 \right)=-1$.
Hàm số đạt cực tiểu tại điểm $x=\pm 1$; giá trị cực tiểu của hàm số là $y\left( \pm 1 \right)=-2$.
Giới hạn của hàm số tại vô cực: $\mathop {\lim }\limits_{x \to – \infty } y = + \infty $, $\mathop {\lim }\limits_{x \to + \infty } y = + \infty .$
Bảng biến thiên:
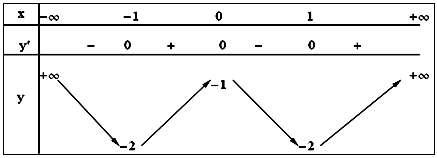
Đồ thị:
Cho $y = – 1 \Rightarrow x = 0$, $x = \pm \sqrt 2 .$
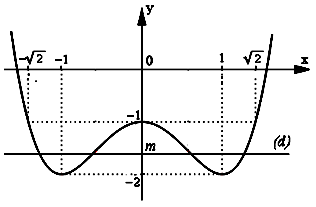
2. Biện luận theo $m$ số nghiệm thực của phương trình:
Số nghiệm của $(*)$ là số giao điểm của $(C)$ và $\left( d \right):y=m$.
Dựa vào đồ thị, ta thấy:
+ Khi $m<-2$ thì $(*)$ vô nghiệm.
+ Khi $\left[ \begin{align}
& m=-2 \\
& m>-1 \\
\end{align} \right.$ thì $(*)$ có $2$ nghiệm.
+ Khi $-2<m<-1$ thì $(*)$ có $4$ nghiệm.
+ Khi $m=-1$ thì (*) có $3$ nghiệm.
Ví dụ 2 . Cho hàm số $y=\frac{1}{2}{{x}^{4}}-m{{x}^{2}}+\frac{3}{2}$ có đồ thị $(C).$
1. Khảo sát sự biến thiên và vẽ đồ thị $(C)$ của hàm số $m=3.$
2. Xác định $m$ để đồ thị của hàm số có cực tiểu mà không có cực đại.
1. Khi $m=3$ thì hàm số là : $y=\frac{1}{2}{{x}^{4}}-3{{x}^{2}}+\frac{3}{2}.$
Tập xác định: $D=\mathbb{R}$.
Chiều biến thiên:
Ta có : $y’=2{{\text{x}}^{3}}-6\text{x}=2\text{x}\left( {{x}^{2}}-3 \right).$
$y’=0\Leftrightarrow 2\text{x}\left( {{x}^{2}}-3 \right)=0$ $\Leftrightarrow \left[ \begin{align}
& x=0 \\
& x=\pm \sqrt{3} \\
\end{align} \right.$
Hàm số đồng biến trên các khoảng $\left( -\sqrt{3};0 \right)$ và $\left( \sqrt{3};+\infty \right)$, nghịch biến trên các khoảng $\left( -\infty ;-\sqrt{3} \right)$ và $\left( 0;\sqrt{3} \right)$.
Hàm số đạt cực đại tại điểm $x=0$; giá trị cực đại của hàm số là $y\left( 0 \right)=\frac{3}{2}$.
Hàm số đạt cực tiểu tại các điểm $x=\pm \sqrt{3}$; giá trị cực tiểu của hàm số là $y\left( \pm \sqrt{3} \right)=-3$.
Giới hạn của hàm số tại vô cực: $\mathop {\lim }\limits_{x \to – \infty } y = + \infty $, $\mathop {\lim }\limits_{x \to + \infty } y = + \infty .$
Bảng biến thiên:
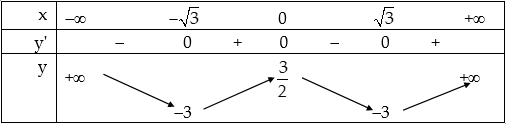
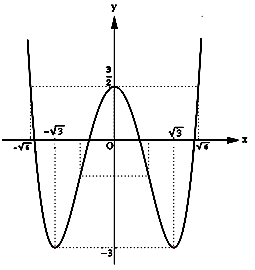
Đồ thị:
Cho $y=\frac{3}{2}$ $\Rightarrow \frac{1}{2}{{x}^{4}}-3{{x}^{2}}=0$ $\Leftrightarrow \left[ \begin{align}
& x=0 \\
& x=\pm \sqrt{6} \\
\end{align} \right.$
Vì hàm số đã cho là hàm số chẵn, nên đồ thị của nó nhận trục tung làm trục đối xứng.
2. Tập xác định: $D=\mathbb{R}.$
Đạo hàm: ${y}’=2{{x}^{3}}-2mx;$ ${y}’=0\Leftrightarrow x=0$ hoặc ${{x}^{2}}=m\left( * \right)$.
Hàm số có cực tiểu mà không có cực đại $⇔ y’ = 0$ có một nghiệm duy nhất và $y’$ đổi dấu từ âm sang dương khi $x$ đi qua nghiệm đó $⇔$ phương trình $(*)$ vô nghiệm hoặc có nghiệm kép $x = 0$ $⇔m≤0.$
Vậy giá trị cần tìm là: $m≤0.$
Ví dụ 3 . Cho hàm số ${\rm{y}} = {{\rm{x}}^{\rm{4}}}–{\rm{2}}\left( {{\rm{m}} + {\rm{1}}} \right){{\rm{x}}^{\rm{2}}} + {\rm{m}}$ có đồ thị $(C).$
1. Khảo sát sự biến thiên và vẽ đồ thị $(C)$ của hàm số khi $m = 1.$
2. Tìm $m$ để đồ thị hàm số $(1)$ có ba điểm cực trị $A$, $B$, $C$ sao cho $OA = BC$; trong đó $O$ là gốc tọa độ, $A$ là điểm cực trị thuộc trục tung, $B$ và $C$ là hai điểm cực trị còn lại.
1. ${\rm{y}} = {{\rm{x}}^{\rm{4}}}–{\rm{ 4}}{{\rm{x}}^{\rm{2}}} + {\rm{1}}$.
Tập xác định D = $\mathbb{R}.$
Sự biến thiên:
Chiều biến thiên: $y’ = 4x^3 – 8x$; $y’ = 0$ $⇔ x = 0$ hoặc $x = \pm \sqrt{2}$.
Hàm số nghịch biến trên các khoảng $(-∞;-\sqrt{2})$ và $(0; \sqrt{2})$; đồng biến trên các khoảng $\left( -\sqrt{2};0 \right)$ và $\left( \sqrt{2};+\infty \right)$.
Cực trị: Hàm số đạt cực tiểu tại $x = ± \sqrt{2}$; ${y_{CT}} = – 3$, đạt cực đại tại $x = 0$; ${y_{CĐ}} = 1$.
Giới hạn: $\mathop {\lim }\limits_{x \to – \infty } y = \mathop {\lim }\limits_{x \to + \infty } y = + \infty $.
Bảng biến thiên:
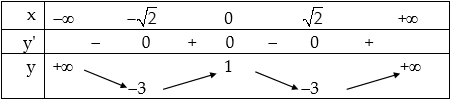
Đồ thị:
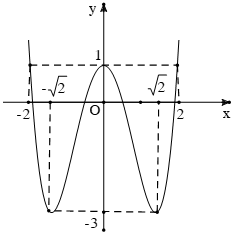
2. Xét $y = x^4 – 2(m + 1)x^2 + m$ $(C_m).$
$y’ = 4x^3 – 4(m + 1)x.$
Đồ thị của hàm số $(C_m)$ có ba cực trị khi và chỉ khi phương trình $y’ = 0$ có ba nghiệm phân biệt.
Ta có: $y’ = 0 ⇔ 4x(x^2 – m – 1) = 0$ $⇔x = 0$ hoặc ${x^2} = m + 1$.
Vì thế để thỏa mãn điều kiện trên thì phương trình $x^2 = m + 1$ cần có hai nghiệm phân biệt khác $0$. Điều đó xảy ra khi và chỉ khi: $m + 1 > 0 ⇔ m > -1$ $(1)$.
Kết luận thỏa mãn $(1)$, $(C_m)$ có ba cực trị tại các điểm: $A(0, m)$, $B\left( { – \sqrt {m + 1} ; – {m^2} – m – 1} \right)$, $C\left( {\sqrt {m + 1} ; – {m^2} – m – 1} \right)$.
Lúc đó: $OA = OB ⇔ OA^2 = BC^2$ (do $OA > 0$; $BC > 0$) $⇔ m^2 = 4(m + 1)$ $⇔ m^2 – 4m – 4 = 0$ $ \Leftrightarrow m = 2 \pm 2\sqrt 2 $.
Ví dụ 4:
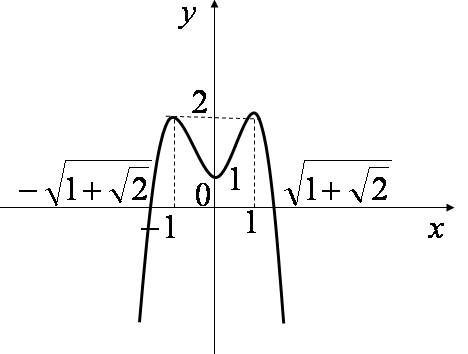
Khảo sát sự biến thiên và vẽ đồ thị hàm số \(y = – {x^4} + 2{x^2} + 1\).
Lời giải:
- Tập xác định: \(D=\mathbb{R}.\)
- \(y’ = – 4{x^3} + 4x\)
\(y’ = 0 \Leftrightarrow – 4{x^3} + 4x = 0 \Leftrightarrow \left[ \begin{array}{l} x = 0\\ {x^2} = 1 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = \pm 1 \end{array} \right.\)
- \(\mathop {\lim }\limits_{x \to – \infty } y = – \infty ;\mathop {\lim }\limits_{x \to + \infty } y = – \infty\)
- Bảng biến thiên:
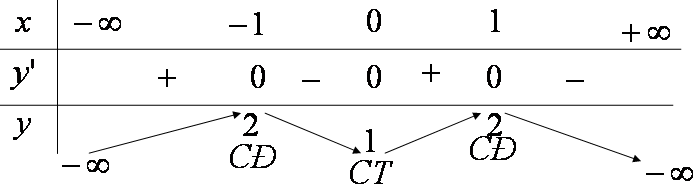
- Vậy:
- Hàm số đồng biến trên các khoảng \(\left( { – \infty ; – 1} \right)\) và \(\left( {0;1} \right).\)
- Hàm số nghịch biến trên các khoảng \((-1;0)\) và \(\left( {1; + \infty } \right)\).
- Hàm số đạt cực đại tại x=-1 và x=1; giá trị cực đại y=2.
- Hàm số đạt cực tiểu tại x=0; giá trị cực tiểu y=1.
- Đồ thị hàm số nhậc trục Oy là trục đối xứng.
\(\begin{array}{l} y = 0 \Leftrightarrow – {x^4} + 2{x^2} + 1 = 0\\ \Rightarrow \left[ \begin{array}{l} {x^2} = 1 + \sqrt 2 \\ {x^2} = 1 – \sqrt 2 (L) \end{array} \right. \Rightarrow x = \pm \sqrt {1 + \sqrt 2 } \end{array}.\)
- Đồ thị hàm số: