[VDC đơn điệu] Cho hàm số $y=f(x)=ax^{4}+bx^{3}+cx^{2}+dx+e \ (a \neq 0)$. Hàm số $y=f'(x)$ có đồ thị như hình vẽ

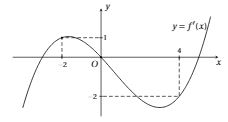
[Hà Nội lần 2] Cho hàm số $y=f(x)=ax^{4}+bx^{3}+cx^{2}+dx+e \ (a \neq 0)$. Hàm số $y=f'(x)$ có đồ thị như hình vẽ

Gọi $S$ là tập hợp tất cả các giá trị nguyên thuộc khoảng $(-6;6)$ của tham số $m$ để hàm số $g(x)=f(3-2x+m)+x^2-(m+3)x+2m^2$ nghịch biến trên khoảng $(0;1)$. Khi đó tổng giá trị các phần tử của $S$ là

A. $12$
B. $9$
C. $6$
D. $15$

LỜI GIẢI

Ta có $g'(x)=-2f'(3-2x+m)+2x-(m+3)$.\\
Đặt $u=3+m-2x$, suy ra $g'(x)=-2f'(u)-u$.\\
Để hàm số $g(x)$ nghịch biến trên khoảng $(0;1)$ khi và chỉ khi
$g'(x)\le 0\ \forall x\in(0;1)$
suy ra
$$-2f'(u)-u\le 0\ \forall u\in(1+m;3+m)\Leftrightarrow f'(u)\ge -\dfrac{u}{2}\ \forall u\in(1+m;3+m). \quad (*)$$

Từ đồ thị hàm số ta có $f'(u)\ge -\dfrac{u}{2}\Leftrightarrow \left[\begin{array}{c} -2 \leq u \leq 0 \\ u \geq 4
\end{array}\right.$
Từ đó suy ra $(*)\Leftrightarrow \left[\begin{array}{c}\begin{cases}-2 \leq 1+m \\
3+m \leq 0\end{cases}\\ 1+m\ge 4
\end{array} \Leftrightarrow\left[\begin{array}{l}
m=-3 \\
m \geq 3
\end{array}\right.\right.$
Vì $m$ là các giá trị nguyên thuộc $(-6;6)$ nên $m\in\{-3;3;4;5\}=S$.
Vậy tổng giá trị các phần tử của $S$ là $-3+3+4+5=9$.