Trả lời câu hỏi trong bài 4 Bất phương trình bậc hai một ẩn – Toán 10 Cánh Diều
=======
LT-VD 1:
a. Cho hai ví dụ về bất phương trình bậc hai một ẩn.
b. Cho hai ví dụ về bất phương trình mà không là bất phương trình bậc hai một ẩn.
Hướng dẫn giải:
a. $x^2-2x+2 > 0$ và $-x^2+5x-3 \leq 0$
b. $4x-1 >0 $ và $-3x +2 \geq 7$
LT-VD 2: Giải các bất phương trình bậc hai sau:
a. $3x^2-2x+4 \leq 0$
b. $-x^2+6x-9 \geq 0$
Hướng dẫn giải:
a. $3x^2-2x+4 \leq 0$
Tam thức bậc hai $3x^2-2x+4$ có $\Delta=-44<0$, hệ số $a=3>0$ nên $f(x)>0$ với $\forall x\in \mathbb{R}$
Vậy bất phương trình $3x^2-2x+4 \leq 0$ vô nghiệm.
b. $-x^2+6x-9 \geq 0$
Tam thức bậc hai $-x^2+6x-9$ có $\Delta=0$, hệ số $a=-1<0$ nên $f(x)<0$ với $\forall x\in \mathbb{R} \setminus \{3\}$
Vậy tập nghiệm của bất phương trình $-x^2+6x-9 \geq 0$ là $\{3\}$.
LT-VD 3: Giải mỗi bất phương trình bậc hai sau bằng cách sử dụng đồ thị:
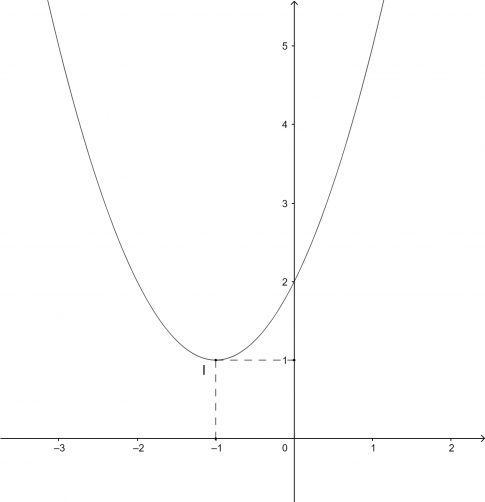
a. $x^2+2x+2>0$
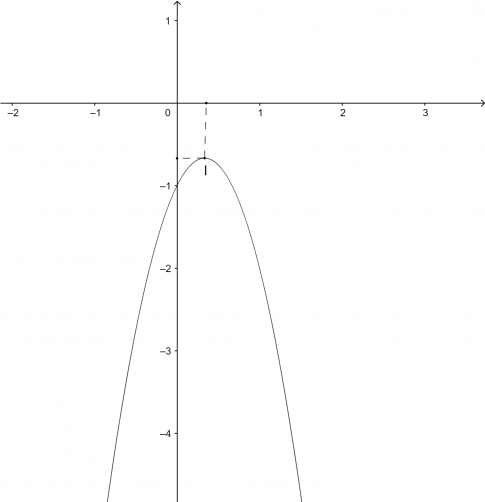
b. $-3x^2+2x-1>0$
Hướng dẫn giải:
a. Từ đồ thị ta thấy $x^2+2x+2>0$ biểu diễn phần parabol $x^2+2x+2=0$ nằm phía trên trục hoành, tương ứng với $x \in \mathbb{R}$
Vậy tập nghiệm của bất phương trình $x^2+2x+2>0$ là $\mathbb{R}$

b. Từ đồ thị ta thấy $-3x^2+2x-1>0$ biểu diễn phần parabol $-3x^2+2x-1=0$ nằm phía trên trục hoành, tương ứng với $x \in \emptyset$
Vậy bất phương trình $-3x^2+2x-1>0$ vô nghiệm.
LT-VD 4: Tổng chi phí $T$ (đơn vị: nghìn đồng) để sản xuất $Q$ sản phẩm được cho bởi biểu thức $T=Q^2+30Q+3300$; giá bán của 1 sản phẩm là 170 nghìn đồng. Số sản phẩm được sản xuất trong khoảng nào để đảm bảo có lãi (giả thiết các sản phẩm được bán hết)?
Hướng dẫn giải:
Theo đầu bài, ta có tổng doanh thu là: $170 Q$ nghìn đồng.
Tổng lợi nhuận là: $170 Q-(Q^2+30Q+3300)$
$=-Q^{2}+140 Q-3300$
Để không bị lỗ thì $-Q^{2}+140 Q-3300 \geq 0$
$-Q^{2}+140 Q-3300=0$ có 2 nghiệm phân biệt $x_{1}=30, x_{2}=110$ và $a=-1<0$
$ \Rightarrow$ Nghiệm của bất phương trình $-Q^{2}+140 Q-3300 \geq 0$ là $30 \leq x \leq 110$
Vậy để có lãi thì số sản phẩm được sản suất nằm trong khoảng $(30;110)$ sản phẩm.
============
Thuộc chủ đề: Học Toán lớp 10 – Cánh diều
