Trả lời câu hỏi trong bài 2 Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng – Toán 10 Cánh Diều

Trả lời câu hỏi trong bài 2 Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng – Toán 10 Cánh Diều

=======

LT-VD 1:  Cho hai ví dụ về hàm số bậc 2.

Hướng dẫn giải:

LT-VD 2:  Vẽ đồ thị mỗi hàm số bậc hai sau:

a. $y=x^2-4x-3$

b. $y=x^2+2x+1$

c. $y=-x^2-2$

Hướng dẫn giải:

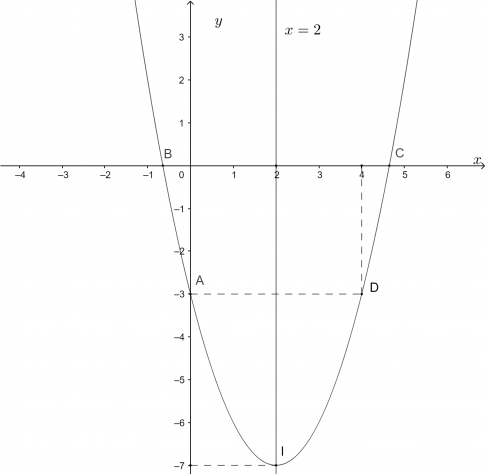
 a. $y=x^2-4x-3$

Ta có: $\Delta=(-4)^{2}-4.1 .(-3)=28$.

• Toạ độ đỉnh $I(2;-7)$.
• Trục đối xứng $x=2$.
• Giao điểm của parabol với trục tung là $A(0 ;-3)$.
• Giao điểm của parabol với trục hoành là $B(2-\sqrt{7}; 0)$ và $C(2+\sqrt{7} ; 0)$.
• Điểm đối xứng với điểm $A(0 ;-3)$ qua trục đối xứng $x=2$ là $D(4;-3)$.

Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số $y=x^2-4x-3$ như hình.

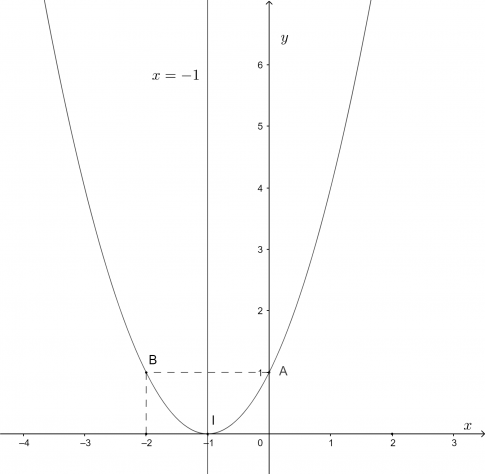
b. $y=x^2+2x+1$

Ta có: $\Delta=2^{2}-4.1.1=0$.

• Toạ độ đỉnh $I(-1;0)$.
• Trục đối xứng $x=-1$.
• Giao điểm của parabol với trục tung là $A(0;1)$.
• Điểm đối xứng với điểm $A(0;1)$ qua trục đối xứng $x=-1$ là $B(-2;1)$.

Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số như hình.

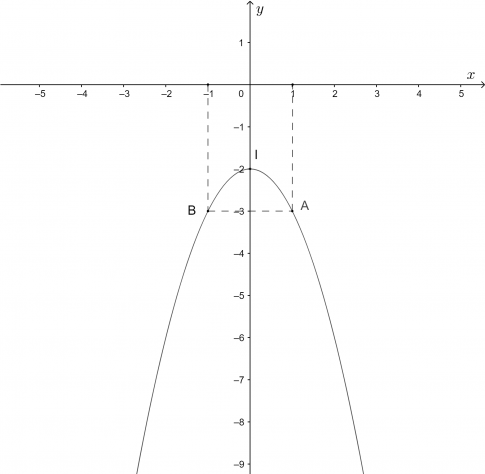
c. $y=-x^2-2$

Ta có: $\Delta=0^{2}-4.(-1).(-2)=-8$.

• Toạ độ đỉnh $I(0;-2)$.
• Trục đối xứng $x=0$.
• Lấy điểm $A(1;-3)$ thuộc đồ thị hảm số, điểm đối xứng với điểm $A(1;-3)$ qua trục đối xứng là $B(-1;-3)$.

Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số như hình.

LT-VD 3:  Lập bảng biến thiên của mỗi hàm số sau:

a. $y=x^2-3x+4$

b. $y=-2x^2+5$

Hướng dẫn giải:

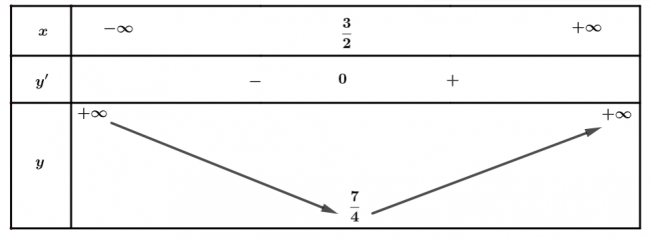
a. $y=x^2-3x+4$

$a=1>0 \Rightarrow$ Hàm số nghịch biến trên khoảng $(−\infty; \frac{3}{2})$ và đồng biến trên $(\frac{3}{2};+\infty)$

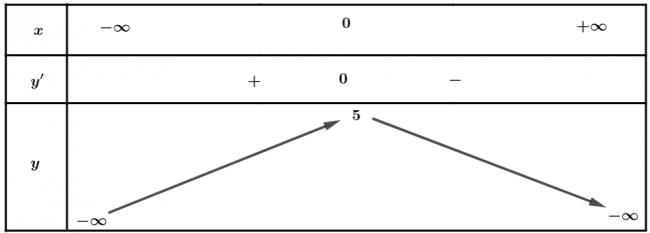
b. $y=-2x^2+5$

$a=-2<0 \Rightarrow$ Hàm số đồng biến trên khoảng $(−\infty; 0)$ và nghịch biến trên $(0;+\infty)$

LT-VD 4:  Trong bài toán ở phần mở đầu, độ cao $y$(m) của một điểm thuộc vòng cung thành cầu cảng Sydney đạt giá trị lớn nhất là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?

Hướng dẫn giải:

Hàm số biểu diễn đồ thị $y=−0,00188(x−251,5)^2+118$

Ta có: $(x−251,5)^2 \geq 0$

$\Leftrightarrow -0,00188(x−251,5)^2 \leq 0$

$\Leftrightarrow −0,00188(x−251,5)^2+118 \leq 118$

Vậy $y_{max}=118$ (m).

============

Thuộc chủ đề: Học Toán lớp 10 – Cánh diều