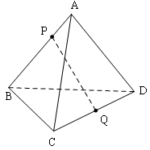
Đề bài: Cho hình tứ diện $ABCD$ trong đó $AB\bot AC, AB\bot BD$. Gọi $P$ và $Q$ là các điểm lần lượt thuộc các đường thẳng $AB$ và $CD$ sao cho $\overrightarrow{PA}=k \overrightarrow{PB}, \overrightarrow{QC}=k \overrightarrow{QD} (k \neq 1)$. Tính góc giữa $AB$ và $PQ.$ Lời giải Ta có … [Đọc thêm...] vềĐề bài: Cho hình tứ diện $ABCD$ trong đó $AB\bot AC, AB\bot BD$. Gọi $P$ và $Q$ là các điểm lần lượt thuộc các đường thẳng $AB$ và $CD$ sao cho $\overrightarrow{PA}=k \overrightarrow{PB}, \overrightarrow{QC}=k \overrightarrow{QD} (k \neq 1)$. Tính góc giữa $AB$ và $PQ.$
Vectơ trong không gian
Đề bài: Cho hình chóp $S.ABCD$ có $SA=a\sqrt{6} $ và vuông góc với mặt phẳng $(ABCD)$ đáy $ABCD$ là nửa lục giác đều nội tiếp trong đường tròn đường kính $AD=2a$$a.$ Tính các khoảng cách từ $A$ và $B$ đến mặt phẳng $(SCD)$$b.$ Tính khoảng cách từ đường thẳng $AD$ đến mặt phẳng $(SBC)$$c.$ Tính diện tích của thiết diện của hình chóp $S.ABCD$ với mặt phẳng $(\alpha) $ song song với mặt phẳng $(SAD)$ và cách một khoảng bằng $\frac{a\sqrt{3} }{4} $
Đề bài: Cho hình chóp $S.ABCD$ có $SA=a\sqrt{6} $ và vuông góc với mặt phẳng $(ABCD)$ đáy $ABCD$ là nửa lục giác đều nội tiếp trong đường tròn đường kính $AD=2a$$a.$ Tính các khoảng cách từ $A$ và $B$ đến mặt phẳng $(SCD)$$b.$ Tính khoảng cách từ đường thẳng $AD$ đến mặt phẳng $(SBC)$$c.$ Tính diện tích của thiết diện của hình chóp $S.ABCD$ với mặt phẳng $(\alpha) $ song song … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABCD$ có $SA=a\sqrt{6} $ và vuông góc với mặt phẳng $(ABCD)$ đáy $ABCD$ là nửa lục giác đều nội tiếp trong đường tròn đường kính $AD=2a$$a.$ Tính các khoảng cách từ $A$ và $B$ đến mặt phẳng $(SCD)$$b.$ Tính khoảng cách từ đường thẳng $AD$ đến mặt phẳng $(SBC)$$c.$ Tính diện tích của thiết diện của hình chóp $S.ABCD$ với mặt phẳng $(\alpha) $ song song với mặt phẳng $(SAD)$ và cách một khoảng bằng $\frac{a\sqrt{3} }{4} $
Đề bài: Cho hình lập phương $ABCD.A'B'C'D'$ cạnh $a$. Gọi $P,Q$ là các điểm xác định bởi $\overrightarrow{AP}=\overrightarrow{D'A}, \overrightarrow{C'Q}=\overrightarrow{DC'}.$ Chứng minh rằng đường thẳng $PQ$ đi qua trung điểm của cạnh $BB'$.
Đề bài: Cho hình lập phương $ABCD.A'B'C'D'$ cạnh $a$. Gọi $P,Q$ là các điểm xác định bởi $\overrightarrow{AP}=\overrightarrow{D'A}, \overrightarrow{C'Q}=\overrightarrow{DC'}.$ Chứng minh rằng đường thẳng $PQ$ đi qua trung điểm của cạnh $BB'$. Lời giải Đặt $\overrightarrow{AA'}=\overrightarrow{a}, … [Đọc thêm...] vềĐề bài: Cho hình lập phương $ABCD.A'B'C'D'$ cạnh $a$. Gọi $P,Q$ là các điểm xác định bởi $\overrightarrow{AP}=\overrightarrow{D'A}, \overrightarrow{C'Q}=\overrightarrow{DC'}.$ Chứng minh rằng đường thẳng $PQ$ đi qua trung điểm của cạnh $BB'$.