Lý thuyết Bài tập cuối chương 5 – Chân trời

Lý thuyết Bài tập cuối chương 5 – Chân trời
============

1.1. Khái niệm vectơ

a) Định nghĩa vectơ

Đại lượng vô hướng là đại lượng chỉ có độ lớn. Ví dụ: khôi lượng, khoảng cách, nhiệt độ, …

Đại lượng có hướng là đại lượng bao gồm cả đô lớn và hướng. Ví du: đô dịch chuyền, lực, vận tốc, gia tộc,

Khi xác định một đại lượng vô hướng, ta chỉ cằn mô tả độ lớn của nó. Ví dụ: Hàng trên tàu có khôi lượng 500 tân.

Khi xác định một đại lượng có hướng, ta phải đề cập đến cả độ lớn và hướng của nó. Ví dụ: Con tàu có độ địch chuyển đài 500 km theo hướng từ A đền B.

Vecto là một đoạn thẳng có hướng, nghĩa là đã chỉ ra điểm đầu và điểm cuối.

* Wectơ có điểm đầu A, điểm cuối B được kí hiệu là \(\overrightarrow {AB} \), đọc là vectơ \(\overrightarrow {AB} \) (Hình sau)

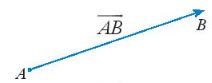
* Đường thẳng đi qua hai điểm A và B gọi là giá của vectơ \(\overrightarrow {AB} \).

* Độ dài của đoạn thẳng AB gọi là độ đài của vectơ V và được kí hiệu là \(\left| {\overrightarrow {AB} {\rm{ }}} \right|\) Như vậy ta có: \(\left| {\overrightarrow {AB} {\rm{ }}} \right| = AB\).

Chú ý: Một vectơ khi không cần chỉ rõ điểm đầu và điểm cuối có thể viết là \(\overrightarrow a ,\overrightarrow b ,\overrightarrow x ,\overrightarrow y \)…

b) Hai vectơ cùng phương, cùng hướng

+) Hai vecto được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.

+) Hai vecto cùng phương thì chúng cùng hướng hoặc ngược hướng.

c) Vectơ bằng nhau – Vectơ đối nhau

+) Hai vecto được gọi là  bằng nhau  nếu chúng có cùng độ dài và cùng hướng.

+) Hai vecto được gọi là  đối nhau  nếu chúng có cùng độ dài và ngược hướng.

Kí hiệu: \(\overrightarrow a  =  – \overrightarrow b \), (vecto \(\overrightarrow b \) là  vecto đối  của vecto \(\overrightarrow a \))

Chú ý: Với mỗi điểm O và vecto \(\overrightarrow a \) cho trước, có duy nhất điểm A sao cho \(\overrightarrow {OA}  = \overrightarrow a \)

d) Vectơ không

Vecto không, là vecto có điểm đầu và điểm cuối trùng nhau. Kí hiệu chung là \(\overrightarrow 0 \).

* Chú ý:

– Vecto không có độ dài bằng 0.

– Vecto \(\overrightarrow 0 \) cùng phương, cùng hướng với mọi vecto.

– Mọi vecto-không đều bằng nhau: \(\overrightarrow 0  = \overrightarrow {AA}  = \;\overrightarrow {BB}  = …\)

– Vecto đối của vecto-không là chính nó.

1.2. Tổng và hiệu của hai vectơ

a) Tổng của hai vectơ

Cho hai vectơ \(\overrightarrow a\) và \(\overrightarrow b\). Từ một điểm A tùy ý, lấy hai điểm B, C sao cho  \(\overrightarrow {AB}  = \overrightarrow a \), \(\overrightarrow {BC}  = \overrightarrow b \). Khi đó \(\overrightarrow {AC} \) được gọi là tổng của hai vecto \(\overrightarrow a\), \(\overrightarrow b\) được kí hiệu là \(\overrightarrow a  + \overrightarrow b \).  Vậy \(\overrightarrow a  + \overrightarrow b  = \overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC} \)

Quy tắc ba điểm:

Với 3 điểm M, N, P ta có: \(\overrightarrow {MN}  + \overrightarrow {NP}  = \overrightarrow {MP} \)

Quy tắc hình bình hành:

Nếu OABC là hình bình hành thì ta có \(\overrightarrow {OA}  + \overrightarrow {OC}  = \overrightarrow {OB} \)

Chú ý:

+ Khi công hai vectơ theo quy tắc ba điểm, điểm cuỗi của vectơ thứ nhât phải là điểm đầu của vectơ thứ hai.

b) Tính chất của phép cộng các vectơ

Phép cộng vecto có các tính chất sau: + Tính chất giao hoán: \(\overrightarrow a  + \overrightarrow b  = \overrightarrow b  + \overrightarrow a \) + Tính chất kết hợp: \((\overrightarrow a  + \overrightarrow b ) + \overrightarrow c  = \overrightarrow a  + (\overrightarrow b  + \overrightarrow c )\) + Với mọi vecto \(\overrightarrow a ,\) ta luôn có: \(\overrightarrow a  + \overrightarrow 0  = \overrightarrow 0  + \overrightarrow a  = \overrightarrow a \)

Chú ý: \(\overrightarrow a  + ( – \overrightarrow a ) = \overrightarrow 0 \) (Tổng hai vecto đối luôn bằng vecto-không)

c) Hiệu của hai vectơ

Hiệu của hai vecto \(\overrightarrow a  – \overrightarrow b  = \overrightarrow a  + \left( { – \overrightarrow b } \right)\)

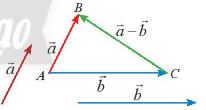
Chú ý: Cho ba điểm O, A, B ta có: \(\overrightarrow {OB}  – \overrightarrow {OA}  = \overrightarrow {AB} \)

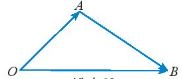
d) Tính chất vectơ của trung điểm đoạn thẳng và trọng tâm tam giác

+) M là trung điểm AB \( \Leftrightarrow \overrightarrow {MA}  + \overrightarrow {MB}  = \overrightarrow 0 \)

+) G là trọng tâm của \(\Delta ABC\) \( \Leftrightarrow \overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0 \)

1.3. Tích của một số với một vectơ

a) Tích của một số với một vecto và các tính chất

+) Tích của một số thực \(k\)với một vecto \(\overrightarrow a  \ne \overrightarrow 0 \) là một vecto, kí kiệu là \(k\overrightarrow a .\) +) Vecto \(k\overrightarrow a \) có độ dài bằng \(\left| k \right|\left| {\overrightarrow a } \right|\) và cùng hướng với vecto \(\overrightarrow a \) nếu \(k > 0\), ngược hướng với vecto \(\overrightarrow a \) nếu \(k < 0\)

+) Quy ước: \(0\;\overrightarrow a  = \overrightarrow 0 \) và \(k\;\overrightarrow 0  = \overrightarrow 0 \)

+) Tính chất: Với hai vecto \(\overrightarrow a ,\overrightarrow b \) và hai số thực \(k,t\) ta luôn có:

 \(\begin{array}{l}k(t\overrightarrow a ) = (kt)\;\overrightarrow a \\(k + t)\,\overrightarrow a  = k\overrightarrow a  + t\overrightarrow a \\k(\overrightarrow a  + \overrightarrow b ) = k\overrightarrow a  + k\overrightarrow b ;\quad k(\overrightarrow a  – \overrightarrow b ) = k\overrightarrow a  – k\overrightarrow b \\1\;\overrightarrow a  = \overrightarrow a ;\;\;( – 1)\;\overrightarrow a  =  – \,\overrightarrow a \end{array}\)

b) Điều kiện để hai vecto cùng phương

Hai vecto \(\overrightarrow a \) và \(\overrightarrow b \) (\(\overrightarrow b \) khác \(\overrightarrow 0 \))cùng phương khi và chỉ khi tồn tại \(k\) sao cho \(\overrightarrow a  = k\overrightarrow b .\)

Nhận xét: Ba điểm phân biệt A, B, C thẳng hàng \( \Leftrightarrow \overrightarrow {AB}  = k\overrightarrow {AC} .\)

Chú ý: Cho hai vecto \(\overrightarrow a \) và \(\overrightarrow b \) không cùng phương. Với mỗi vecto \(\overrightarrow c \) luôn tồn tại duy nhất cặp số thực \((m;n)\) sao cho \(\overrightarrow c  = m\,\overrightarrow a  + n\,\overrightarrow b \) 

1.4. Tích vô hướng của hai vectơ

a) Góc giữa hai vectơ

Cho hai vecto \(\overrightarrow u \) và \(\overrightarrow v \) khác \(\overrightarrow 0 \). Góc giữa hai vecto \(\overrightarrow u \) và \(\overrightarrow v \) , kí hiệu \(\left( {\;\overrightarrow u ,\overrightarrow v } \right)\) *Cách xác định góc Chọn điểm A bất kì, vẽ \(\overrightarrow {AB}  = \overrightarrow u \) và \(\overrightarrow {AC}  = \overrightarrow v \). Khi đó \(\left( {\;\overrightarrow u ,\overrightarrow v } \right) = \widehat {BAC}\).

* Các trường hợp đặc biệt:

+) \(\left( {\;\overrightarrow u ,\overrightarrow 0 } \right) = \alpha \) tùy ý, với \({0^ \circ } \le \alpha  \le {180^ \circ }\)

+) \(\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {90^ \circ } \Leftrightarrow \overrightarrow u  \bot \overrightarrow v \) hoặc \(\overrightarrow v  \bot \overrightarrow u \). Đặc biệt: \(\overrightarrow 0  \bot \overrightarrow u \;\;\forall \overrightarrow u \;\)

+) \(\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {0^ \circ } \Leftrightarrow \overrightarrow u ,\overrightarrow v \) cùng hướng

+) \(\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {180^ \circ } \Leftrightarrow \overrightarrow u ,\overrightarrow v \) ngược hướng

Chú ý:

– Từ định nghĩa ta có \(\left( {\overrightarrow a ,\overrightarrow b } \right) = \left( {\overrightarrow b ,\overrightarrow a } \right)\)

– Góc giữa hai vectơ cùng hướng và khác \({\overrightarrow 0 }\) luôn bằng 00

– Góc giữa hai vectơ ngược hướng và khác \({\overrightarrow 0 }\) luôn bằng 1800,

– Trong trường hợp có ít nhất một trong hai vectơ \({\overrightarrow a }\) hoặc \({\overrightarrow b }\) là vectơ \({\overrightarrow 0 }\) thì ta quy ước

số đo góc giữa hai vectơ đó là tuỷ ý (từ 00 đến 1800)

b) Tích vô hướng của hai vectơ

Tích vô hướng của hai vecto \(\overrightarrow u ,\;\overrightarrow v \): \(\overrightarrow u .\;\overrightarrow v  = \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right|.\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)\)

Chú ý:

+) \(\overrightarrow u .\;\overrightarrow v \;\; = 0 \Leftrightarrow \overrightarrow u  \bot \;\overrightarrow v \;\;\)

+) \(\overrightarrow u .\;\overrightarrow u \;\; = {\overrightarrow u ^2} = \left| {\overrightarrow u } \right|.\left| {\overrightarrow u } \right|.\cos {0^ \circ } = {\left| {\overrightarrow u } \right|^2}\)

c) Tính chất của tích vô hướng

Cho 3 vecto \(\overrightarrow u ,\overrightarrow v ,\overrightarrow w \) bất kì và mọi số thực k, ta có: \(\begin{array}{l}\overrightarrow u .\;\overrightarrow v \;\; = \overrightarrow v .\;\overrightarrow u \;\\\overrightarrow u .\;\left( {\overrightarrow v  + \overrightarrow w \;} \right)\; = \overrightarrow u .\;\overrightarrow v \; + \overrightarrow u .\;\overrightarrow w \;\\\left( {k\overrightarrow u } \right).\overrightarrow v  = k.\left( {\overrightarrow u .\;\overrightarrow v \;} \right) = \overrightarrow u .\;\left( {k\overrightarrow v \;} \right)\end{array}\)

Nhận xét

\(\begin{array}{l}\overrightarrow u .\;\left( {\overrightarrow v  – \overrightarrow w \;} \right)\; = \overrightarrow u .\;\overrightarrow v \; – \overrightarrow u .\;\overrightarrow w \\{\left( {\overrightarrow u  + \overrightarrow v } \right)^2}\;\; = {\overrightarrow u ^2} + 2\overrightarrow u .\;\overrightarrow v \; + \;{\overrightarrow v ^2};\;\;{\left( {\overrightarrow u  – \overrightarrow v } \right)^2}\;\; = {\overrightarrow u ^2} – 2\overrightarrow u .\;\overrightarrow v \; + \;{\overrightarrow v ^2}\\\left( {\overrightarrow u  + \overrightarrow v } \right)\left( {\overrightarrow u  – \overrightarrow v } \right) = {\overrightarrow u ^2} – {\overrightarrow v ^2}\end{array}\)

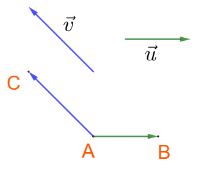
Câu 1: Quan sát Hình sau và gọi tên các vectơ:

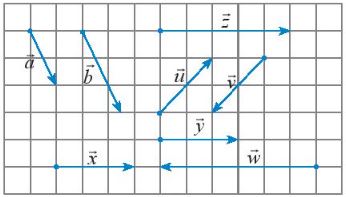
a) Cùng phương với vectơ \(\overrightarrow x \);

b) Cùng hướng với vectơ \(\overrightarrow a \) ;

Ngược hướng với vectơ  \(\overrightarrow u \).

Hướng dẫn giải

a) Ta có:

Giá của vectơ \(\overrightarrow {\rm{w}} \) trùng với giá của \(\overrightarrow x \)

Giá của vectơ \(\overrightarrow y \), \(\overrightarrow z \)song song với giá của \(\overrightarrow x \)

Suy ra các vectơ cùng phương với vectơ \(\overrightarrow x \) là \(\overrightarrow {\rm{w}} \), \(\overrightarrow y \)và \(\overrightarrow z \)

b) Ta có:

Vectơ \(\overrightarrow b \) có giá song song với vectơ \(\overrightarrow a \)và có cùng hướng từ trên xuống với vectơ \(\overrightarrow a \)nên vectơ \(\overrightarrow b \) cùng hướng với vectơ \(\overrightarrow a \)

c) Ta có:

Vectơ \(\overrightarrow v \) có giá song song với vectơ \(\overrightarrow u \)và ngược hướng từ dưới lên trên so với vectơ \(\overrightarrow u \)nên vectơ \(\overrightarrow v \) ngược hướng với vectơ \(\overrightarrow u \)

Câu 2: Cho tam giác đều ABC cạnh có độ dài là a. Tính độ dài vectơ \(\overrightarrow {AB}  + \overrightarrow {AC}\) 

Hướng dẫn giải

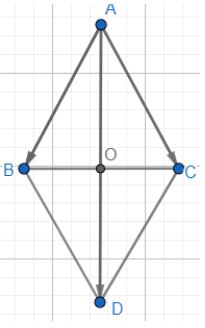
Áp dụng quy tắc hình bình hành vào ABDC ta có:

\(\overrightarrow {AB}  + \overrightarrow {AC}  = \overrightarrow {AD}  \Rightarrow \left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD\)

Gọi O là giao điểm của AD và BC, ta có:

\(AO = \sqrt {A{B^2} – B{O^2}}  = \sqrt {A{B^2} – {{\left( {\frac{1}{2}BC} \right)}^2}}  = \sqrt {{a^2} – {{\left( {\frac{a}{2}} \right)}^2}}  = \frac{{a\sqrt 3 }}{2}\)

\(AD = 2AO = a\sqrt 3  \Rightarrow \left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = a\sqrt 3 \)

Vậy độ dài vectơ \(\overrightarrow {AB}  + \overrightarrow {AC} \) là \(a\sqrt 3 \)

Câu 3: Cho hình vuông ABCD có cạnh bằng 1. Tính độ dài các vectơ sau:

a) \(\overrightarrow a  = \left( {\overrightarrow {AC}  + \overrightarrow {BD} } \right) + \overrightarrow {CB} ;\)                       

b) \(\overrightarrow a  = \overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {BC}  + \overrightarrow {DA} .\) 

Hướng dẫn giải

a) \(\begin{array}{l}\overrightarrow a  = \left( {\overrightarrow {AC}  + \overrightarrow {BD} } \right) + \overrightarrow {CB}  = \left( {\overrightarrow {AC}  + \overrightarrow {CB} } \right) + \overrightarrow {BD} \\ = \overrightarrow {AB}  + \overrightarrow {BD}  = \overrightarrow {AD}  \Rightarrow \left| {\overrightarrow {AD} } \right| = AD = 1\end{array}\)

b) \(\begin{array}{l}\overrightarrow a  = \overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {BC}  + \overrightarrow {DA}  = \left( {\overrightarrow {AB}  + \overrightarrow {BC} } \right) + \left( {\overrightarrow {AD}  + \overrightarrow {DA} } \right)\\ = \overrightarrow {AC}  + \overrightarrow {AA}  = \overrightarrow {AC}  + \overrightarrow 0  = \overrightarrow {AC} \end{array}\)

\(AC = \sqrt {A{B^2} + B{C^2}}  = \sqrt {{1^2} + {1^2}}  = \sqrt 2 \)

\( \Rightarrow \left| {\overrightarrow {AC} } \right| = \sqrt 2 \)

Câu 4: Cho tứ giác ABCD có I và J lần lượt là trung điểm của AB và CD. Cho điểm G thỏa mãn \(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD}  = \overrightarrow 0 \). Chứng minh ba điểm I, G, J  thẳng hàng

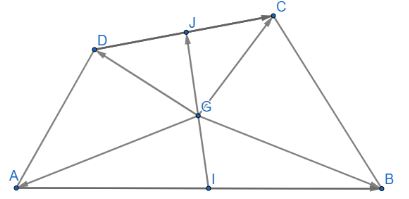
Hướng dẫn giải

Ta có:

\(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD}  = \overrightarrow 0  \Leftrightarrow \left( {\overrightarrow {GI}  + \overrightarrow {IA} } \right) + \left( {\overrightarrow {GI}  + \overrightarrow {IB} } \right) + \left( {\overrightarrow {GJ}  + \overrightarrow {JC} } \right) + \left( {\overrightarrow {GJ}  + \overrightarrow {JD} } \right) = \overrightarrow 0 \)

\( \Leftrightarrow 2\overrightarrow {GI}  + \left( {\overrightarrow {IA}  + \overrightarrow {IB} } \right) + 2\overrightarrow {GJ}  + \left( {\overrightarrow {JC}  + \overrightarrow {JD} } \right) = \overrightarrow 0 \)

\( \Leftrightarrow 2\overrightarrow {GI}  + 2\overrightarrow {GJ}  = \overrightarrow 0  \Leftrightarrow 2\left( {\overrightarrow {GI}  + \overrightarrow {GJ} } \right) = \overrightarrow 0 \)

\( \Leftrightarrow \overrightarrow {GI}  + \overrightarrow {GJ}  = \overrightarrow 0  \Rightarrow \)G là trung điểm của đoạn thẳng IJ

Vậy I, G, J thẳng hàng

Câu 5: Cho hai vectơ \(\overrightarrow i ,\overrightarrow j \) vuông góc có cùng độ dài bằng 1.

a) Tính \({\left( {\overrightarrow i  + \overrightarrow j } \right)^2};{\left( {\overrightarrow i  – \overrightarrow j } \right)^2};\left( {\overrightarrow i  + \overrightarrow j } \right)\left( {\overrightarrow i  – \overrightarrow j } \right)\).

b) Cho \(\overrightarrow a  = 2\overrightarrow i  + 2\overrightarrow j ,\overrightarrow b  = 3\overrightarrow i  – 3\overrightarrow j \). Tính tích vô hướng \(\overrightarrow a .\overrightarrow b \) và tính góc \(\left( {\overrightarrow a ,\overrightarrow b } \right)\)

Hướng dẫn giải

a) Ta có hai vectơ \(\overrightarrow i \) và \(\overrightarrow j \) vuông góc nên \(\overrightarrow i .\overrightarrow j  = 0\)

+) \({\left( {\overrightarrow i  + \overrightarrow j } \right)^2} = {\left( {\overrightarrow i } \right)^2} + {\left( {\overrightarrow j } \right)^2} + 2\overrightarrow i .\overrightarrow j  = {\left| {\overrightarrow i } \right|^2} + {\left| {\overrightarrow j } \right|^2} = 1 + 1 = 2\)

+) \({\left( {\overrightarrow i  + \overrightarrow j } \right)^2} = {\left( {\overrightarrow i } \right)^2} + {\left( {\overrightarrow j } \right)^2} – 2\overrightarrow i .\overrightarrow j  = {\left| {\overrightarrow i } \right|^2} + {\left| {\overrightarrow j } \right|^2} = 1 + 1 = 2\)

+) \(\left( {\overrightarrow i  + \overrightarrow j } \right)\left( {\overrightarrow i  – \overrightarrow j } \right) = {\left( {\overrightarrow i } \right)^2} – {\left( {\overrightarrow j } \right)^2} = {\left| {\overrightarrow i } \right|^2} – {\left| {\overrightarrow j } \right|^2} = 1 – 1 = 0\)

b) Sử dụng kết quả của câu a) ta có:

\(\overrightarrow a .\overrightarrow b  = \left( {2\overrightarrow i  + 2\overrightarrow j } \right).\left( {3\overrightarrow i  – 3\overrightarrow j } \right) = 2.3.\left( {\overrightarrow i  + \overrightarrow j } \right).\left( {\overrightarrow i  – \overrightarrow j } \right) = 6.0 = 0\)

\(\overrightarrow a .\overrightarrow b  = 0 \Rightarrow \overrightarrow a  \bot \overrightarrow b  \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = 90^\circ \)

===========
Chuyên mục: Chương 5: Vectơ