Giải Câu hỏi 1 trang 59 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Tìm phương án Sai trong câu sau: Trong tam giác
A.đối diện với góc lớn nhất là cạnh lớn nhất
B.đối diện với cạnh bé nhất là góc nhọn
C.đối diện với cạnh lớn nhất là góc tù
D.đối diện với góc tù (nếu có) là cạnh lớn nhất.
Phương pháp giải:
Quan hệ giữa góc và cạnh đối diện trong một tam giác
Lời giải chi tiết:
Chọn C
–>
— *****
Giải Câu hỏi 2 trang 59 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Bộ ba số nào sau đây không là độ dài ba cạnh của một tam giác?
A.7, 5, 7
B.7, 7, 7
C.3, 5, 4
D.4, 7, 3
Phương pháp giải:
Áp dụng bất đẳng thức tam giác
Nếu cạnh lớn nhất nhỏ hơn tổng 2 cạnh còn lại thì bộ ba số có là độ dài ba cạnh của một tam giác.
Lời giải chi tiết:
4 + 3 = 7 => Bộ ba số 4,7,3 không là độ dài ba cạnh của một tam giác.
Chọn D
–>
— *****
Giải Câu hỏi 3 trang 59 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Tam giác cân có độ dài cạnh bên b, độ dài cạnh đáy d thì ta phải có:
A.d > b
B.d = 2b
C.d < b/2
D. d < 2b
Phương pháp giải:
Áp dụng bất đẳng thức tam giác
Trong tam giác cân, 2 cạnh bên bằng nhau
Lời giải chi tiết:
Tam giác có 2 cạnh bên là b, áp dụng bất đẳng thức trong tam giác:
b + b > d => 2b > d.
Chọn D
–>
— *****
Giải Câu hỏi 4 trang 59 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Với mọi tam giác ta đều có:
A.mỗi cạnh lớn hơn nửa chu vi
B.mỗi cạnh lớn hơn hoặc bằng nửa chu vi
C.mỗi cạnh nhỏ hơn nửa chu vi
D.cả ba trường hợp trên đều có thể xảy ra.
Phương pháp giải:
Áp dụng bất đẳng thức tam giác
Lời giải chi tiết:
Ba cạnh bất kì trong tam giác:a, b, c
Theo bất đẳng thức tam giác: a < b + c =>a + a < a + b + c
Vậy mỗi cạnh nhỏ hơn nửa chu vi.
–>
— *****
Giải Câu hỏi 5 trang 59 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Xét hai đường trung tuyến BM, CN của tam giác ABC có BC = 4cm. Trong các số sau, số nào có thể là tổng độ dài BM + CN?
A.5 cm
B.5,5 cm
C.6 cm
D.6,5 cm
Phương pháp giải:
Áp dụng bất đẳng thức tam giác
Tính chất trọng tâm tam giác
Lời giải chi tiết:
G là trọng tâm tam giác ABC
Xét tam giác GBC có GB + GC > BC ( Bất đẳng thức tam giác)
\(\begin{array}{l} \Rightarrow \dfrac{2}{3}\left( {BM + CN} \right) > BC\\ \Rightarrow BM + CN > \dfrac{3}{2}BC = 6\end{array}\)
Chọn D.
–>
— *****
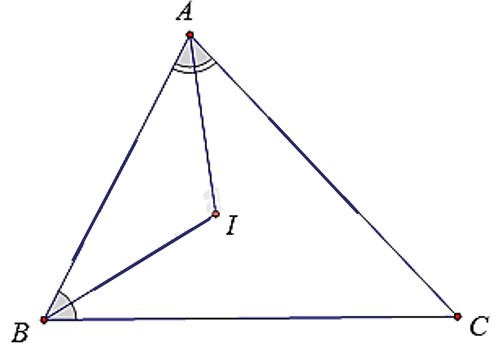
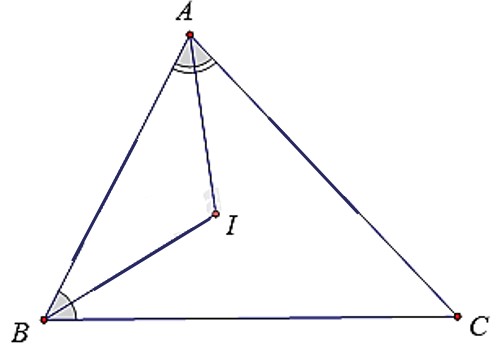
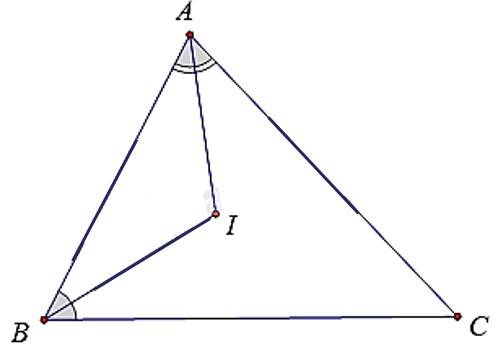
Giải Câu hỏi 6 trang 59 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Tam giác ABC có số đo ba góc thoả mãn: \(\widehat A = \widehat B + \widehat C\). Hai tia phân giác của góc A và góc B cắt nhau tại điểm I. Khi đó góc BIC có số đo là:
A.\({120^0}\)
B. \({125^0}\)
C. \({130^0}\)
D. \({135^0}\)
Phương pháp giải:
Áp dụng định lí về tổng ba góc trong tam giác; tính chaasrt tia phân giác của một góc.
Lời giải chi tiết:

Ta có:
\(\widehat A + \widehat B + \widehat C = {180^0}\)(Tổng ba góc trong tam giác)
Mà \(\widehat A = \widehat B + \widehat C\)
\(\begin{array}{l} \Rightarrow \left( {\widehat B + \widehat C} \right) + \widehat B + \widehat C = {180^0}\\ \Rightarrow 2\left( {\widehat B + \widehat C} \right) = {180^0}\\ \Rightarrow \widehat B + \widehat C = {180^0}:2 = {90^0}\\ \Rightarrow \widehat A = \widehat B + \widehat C = {90^0}\end{array}\)
Xét tam giác BIC có:
\(\widehat {BIC} = {180^0} – \left( {\widehat {\dfrac{B}{2}} + \dfrac{{\widehat C}}{2}} \right) = {180^0} – \dfrac{{{{90}^0}}}{2} = {180^0} – {45^0} = {135^0}\).
Chọn D.
–>
— *****
Giải bài 9.23 trang 60 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Cho D là một điểm bên trong tam giác ABC. Chứng minh:
a)\(\widehat {BDC} > \widehat {BAC}\)
b) BD + DC < AB + AC
Phương pháp giải:
a)
– Tia AD chia góc A thành góc A1 và góc A2, chia góc BDC thành góc D1 và góc D2.
-Áp dụng tính chất góc ngoài của tam giác
b)
– Gọi E là giao điểm của BD và AC. Ta có:
AB + AC = AB + (AE + EC) = (AB + AE) + EC
-Áp dụng các bất đẳng thức cho tam giác: ABE, DEC
Lời giải chi tiết:
a)
Tia AD chia góc A thành góc A1 và góc A2, chia góc BDC thành góc D1 và góc D2.
Góc D1 là góc ngoài tại đỉnh D của tam giác ABD nên:
\(\widehat {{D_1}} > \widehat {{A_1}}\)
Góc D2 là góc ngoài tại đỉnh D của tam giác ADC nên:
\(\widehat {{D_2}} > \widehat {{A_2}}\)
\( \Rightarrow \widehat D = \widehat {{D_1}} + \widehat {{D_2}} > \widehat {{A_1}} + \widehat {{A_2}} = \widehat A\)
b)

Gọi E là giao điểm của BD và AC. Ta có:
AB + AC = AB + (AE + EC) = (AB + AE) + EC
Mà: AB + AE > BE (bất đẳng thức trong tam giác ABE)
=>(AB + AE) + EC > BE + EC = (BD + DE) + EC = BD + (DE + EC)
Mà DE + EC > DC (bất đẳng thức trong tam giác DEC)
=>AB + AC > BD + DC.
–>
— *****
Giải bài 9.24 trang 60 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Cho M là một điểm tuỳ ý bên trong tam giác đều ABC. Lấy điểm N nằm khác phía với M đối với đường thẳng AC sao cho \(\widehat {CAN} = \widehat {BAM}\) và AN = AM.
Chứng minh:
a) Tam giác AMN là tam giác đều
b) \(\Delta MAB = \Delta NAC\)
c) MN = MA, NC = MB
Phương pháp giải:
a)Tam giác AMN cân có 1 góc bằng 60 độ
b) Cm: \(\Delta MAB = \Delta NAC\) (c – g – c )
c) Áp dụng ý a, b.
Lời giải chi tiết
a)
Tam giác ABC là tam giác đều nên: \(\widehat A = \widehat B = \widehat C = {60^0}\)
Ta có:
\(\begin{array}{l}\widehat {MAN} = \widehat {MAC} + \widehat {CAN} = \widehat {MAC} + \widehat {BAM}\left( {do\,\,\widehat {CAN} = \widehat {BAM}} \right)\\ \Rightarrow \widehat {MAN} = \widehat {BAC} = {60^0}\end{array}\)
Xét tam giác AMN có: AM = AN (gt)
\( \Rightarrow \Delta AMN\) cân tại A
Mà \(\widehat {MAN} = {60^0} \Rightarrow \Delta ABC\) là tam giác đều.
b)
Xét \(\Delta MAB\) và \(\Delta NAC\) có:
AB = AC (gt)
AM = AN (gt)
\(\widehat {MAB} = \widehat {NAC}\)(gt)
\( \Rightarrow \)\(\Delta MAB\)= \(\Delta NAC\) (c – g – c)
c)
Tam giác AMN đều (cm ý a)
\( \Rightarrow \)MN = MA
\(\Delta MAB\)= \(\Delta NAC\) (cm ý b)
\( \Rightarrow MB = NC\)(cạnh tương ứng)
–>
— *****
Giải bài 9.25 trang 60 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Xét tam giác ABC vuông tại A; đường phân giác góc B cắt cạnh AC tại E; đường thẳng qua E vuông góc với BC cắt đường thẳng AB tại K. Chứng minh:
a)AE < EC
b) BK = BC.
Phương pháp giải:
a)
-Chứng minh: EA = EH (Điểm nằm trên tia phân giác của góc thì cách đều 2 cạnh của góc đó).
-Áp dụng mối liên hệ giữa cạnh huyền và cạnh góc vuông.
b)
Chứng minh tam giác BCK cân tại B.
Lời giải chi tiết:
a)
Đường thẳng EK cắt BC tại H
Ta có: E nằm trên đường phân giác góc B
\( \Rightarrow EA = EH\)(T/c)
Lại có: Tam giác EHC vuông tại H có: EH là cạnh góc vuông, EC là cạnh huyền
\( \Rightarrow EH < EC\) (mlh giữa cạnh huyền và cạnh góc vuông)
\( \Rightarrow EA < EC\).
b)
Xét tam giác BCK có:
\(\left\{ \begin{array}{l}KH \bot BC\\CA \bot BK\end{array} \right.\)
\( \Rightarrow \)CH, BK là đường cao trong tam giác BCK
Mà CH cắt BK tại E
\( \Rightarrow \)E là trực tâm tam giác BCK
\( \Rightarrow \)BE là đường cao
\( \Rightarrow \) BE vừa là đường phân giác, vừa là đường cao xuất phát từ B của tam giác BCK
\( \Rightarrow \)Tam giác BCK cân tại B.
\( \Rightarrow \)BC = BK.
–>
— *****
Giải bài 9.26 trang 60 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Cho C là trung điểm của đoạn thẳng AB. Gọi Ax, By là hai đường thẳng vuông góc với AB tại A và tại B. Một đường thẳng qua C cắt Ax tại M, cắt By tại P. Điểm N nằm trên tia đối của tia BP sao cho góc MCN là góc vuông. Gọi H là hình chiếu của C trên MN.
Chứng minh:
a)AM + BN = MN;
b) CM là đường trung trực của AH, CN là đường trung trực của BH;
c) Góc AHB là góc vuông.
Phương pháp giải:
a)
-Chứng minh AM = MH: \(\Delta AMC = \Delta HMC\)
-Chứng minh:NB = NH:\(\Delta CHN = \Delta CBN\left( {ch – gn} \right)\)
b)Áp dụng kết quả ý a
c)Trong tam giác đường trung tuyến ứng với 1 cạnh và bằng nửa cạnh đó thì tam giác đó là tam giác vuông
Lời giải chi tiết:
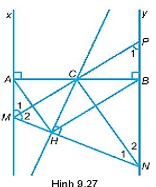
a)
-Chứng minh AM = MH
Xét \(\Delta AMC\) và \(\Delta BPC\) có:
AC = CB (gt)
\(\widehat {MAC} = \widehat {PBC} = {90^0}\)
\(\widehat {ACM} = \widehat {BCP}\)(đối đỉnh)
\( \Rightarrow \)\(\Delta AMC\) = \(\Delta BPC\)(g – c – g)
\( \Rightarrow \) MC = CP (cạnh tương ứng)
Mà \(NC \bot MP\)
\( \Rightarrow \)NC là đường trung trực của MP
\( \Rightarrow \)Tam giác NMP cân tại N
\( \Rightarrow \)\(\widehat {{P_1}} = \widehat {{M_2}}\)
Mà \(\widehat {{P_1}} = \widehat {{M_1}}\)(so le trong: Mx // By)
\( \Rightarrow \widehat {{M_1}} = \widehat {{M_2}}\)
Xét \(\Delta AMC\) và \(\Delta HMC\) có:
\(\begin{array}{l}\widehat {MAC} = \widehat {MHC} = {90^0}\\MC:chung\\\widehat {{M_1}} = \widehat {{M_2}}\left( {cmt} \right)\\ \Rightarrow \Delta AMC = \Delta HMC\left( {ch – gn} \right)\\ \Rightarrow AM = MH\left( {ctu} \right)\end{array}\)
-Chứng minh:NB = NH
Tam giác MNP cân tại N có NC là đường trung trực đồng thời là đường phân giác xuất phát từ N.
Xét \(\Delta HNC\) và \(\Delta BNC\) có:
CN: chung
\(\begin{array}{l}\widehat {{N_1}} = \widehat {{N_2}}\left( {cmt} \right)\\\widehat {CHN} = \widehat {CBN} = {90^0}\\ \Rightarrow \Delta CHN = \Delta CBN\left( {ch – gn} \right)\end{array}\)
\( \Rightarrow NH = NB\)(cạnh tương ứng)
\( \Rightarrow AM + BN = MH + HN = MN\)
b)
Tam giác MAH cân tại M với MC là đường phân giác xuất phát từ đỉnh cân M
\( \Rightarrow \)MC là đồng thời là đường trung trực của AH
Tam giác NBH cân tại N với NC là đường phân giác xuất phát từ đỉnh cân N
\( \Rightarrow \)NC đồng thời là đường trung trực của BH.
c)
Xét tam giác HAB có CA = CB
\( \Rightarrow \)HC là đường trung tuyến
\(\Delta AMC = \Delta HMC\)(cmt) \( \Rightarrow AC = HC\)(cạnh tương ứng)
\( \Rightarrow HC = CA = CB\)
Đường trung tuyến ứng với cạnh AB và bằng nửa cạnh AB.
Vậy tam giác HAB vuông tại H.
–>
— *****
