Giải bài 9.1 trang 48 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Tam giác ABC có cạnh BC dài nhất. Chứng minh số đo góc A lớn hơn hoặc bằng \({60^0}\)
Phương pháp giải:
Áp dụng mối liên hệ giữa cạn và góc trong tam giác: Góc đối diện với cạnh lớn hơn là góc lớn hơn.
Lời giải chi tiết:
Do cạnh BC dài nhất nên góc A lớn nhất (mối liên hệ giữa cạnh và góc trong tam giác)
\( \Rightarrow \)\(\left\{ \begin{array}{l}\widehat A \ge \widehat B\\\widehat A \ge \widehat C\end{array} \right.\)
Nếu \(\widehat A < {60^0} \Rightarrow \widehat B < {60^0};\widehat C < {60^0}\)
\( \Rightarrow \widehat A + \widehat B + \widehat C < {60^0} + {60^0} + {60^0} = {180^0}\) (Vô lí)
Vậy \(\widehat A \ge {60^0}\)
–>
— *****
Giải bài 9.2 trang 48 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
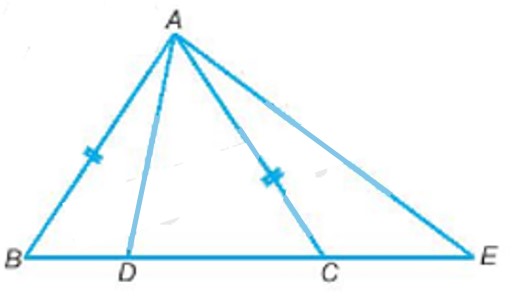
Cho tam giác ABC cân tại A, hai điểm D, E nằm trên đường thẳng BC, D nằm giữa B và C, C nằm giữa D và E. Hãy chứng minh AD < AC < AE.
Phương pháp giải:
-Xét AD vuông góc với BC
-AD không vuông góc với BC
-Chỉ ra các góc tù
-Áp dụng mối liên hệ giữa cạnh và góc trong tam giác
Lời giải chi tiết:

TH1: \(AD \bot BC\)
Khi đó: AC là cạnh huyền, AD là cạnh góc vuông
Nên: AD < AC.
TH2: AD không vuông góc với BC.
Trong 2 góc bù nhau ADB và ADC có 1 góc tù (Hình 9.12): Tam giác ADB là tam giác tù
Cạnh AB đối diện với góc tù ADB nên AD < AB = AC (mối liên hệ giữa cạnh và góc trong tam giác)
Ngược lại, chứng minh tương tự khi tam giác ADC là tam giác tù: AD < AC
Vậy ta luôn có AD < AC (1)
Xét tam giác ACE có góc ACE là góc tù (bù với góc nhọn ACB)
Nên AE > AC (mối liên hệ giữa cạnh và góc trong tam giác) (2)
Từ (1) và (2) suy ra AD < AC < AE.
–>
— *****
Giải bài 9.3 trang 48 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Hãy giải thích tại sao trong tam giác vuông, cạnh huyền dài nhất và trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất
Phương pháp giải:
Trong tam giác vuông, góc vuông là góc lớn nhất do hai góc còn lại đều là góc nhọn, nên cạnh đối điện với nó là cạnh huyền dài nhất
Tương tự, trong tam giác tù có một góc tù thì 2 góc còn lại đều nhọn nên góc tù là góc lớn nhất; vậy cạnh đối diện góc tù là cạnh lớn nhất.
Lời giải chi tiết:
-Xét tam giác ABC vuông tại B:
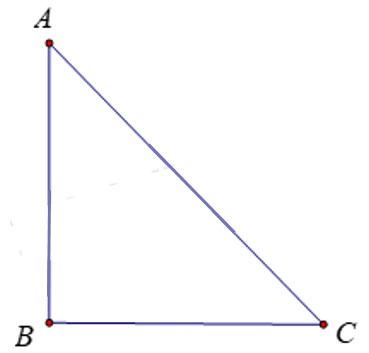
\(\widehat B = {90^0} \Rightarrow \left\{ \begin{array}{l}\widehat B > \widehat A\\\widehat B > \widehat C\end{array} \right.\)
Mà cạnh đối diện với góc vuông là AC
Vậy cạnh huyền AC lớn nhất (mối liên hệ giữa cạnh và góc trong tam giác)
-Xét tam giác tù ABC với góc A là góc tù:
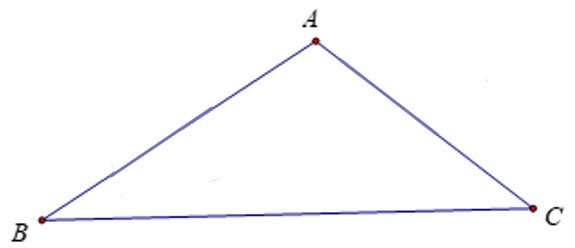
\( \Rightarrow \widehat B,\widehat C\) là góc nhọn.
\( \Rightarrow \widehat A\)là góc lớn nhất.
Cạnh đối diện với góc A là cạnh BC
\( \Rightarrow BC\)là cạnh lớn nhất (mối liên hệ giữa cạnh và góc trong tam giác)
–>
— *****
Giải bài 9.4 trang 48 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Cho tam giác ABC với AB > AC. Gọi M là trung điểm của cạnh BC.
a)Hãy so sánh hai góc MAB và MAC.
b)Tia phân giác của góc BAC cắt BC tại D. Hỏi D thuộc đoạn thẳng MB hay đoạn thẳng MC? Vì sao?
Phương pháp giải:
a)
– Lấy điểm P sao cho M là trung điểm của AP.
-Chứng minh: \(\Delta AMC = \Delta PMB\left( {c – g – c} \right)\)
-Chứng minh: \(\widehat {MPB} > \widehat {MAB}\)
Lời giải chi tiết:
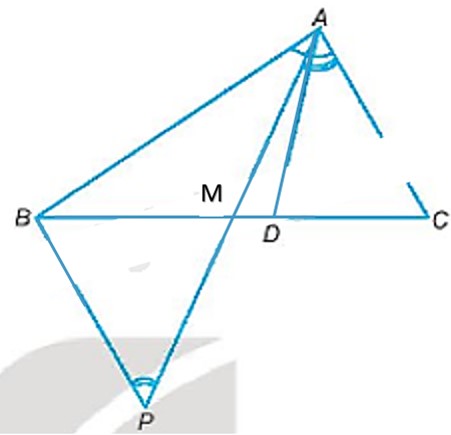
a)
Lấy điểm P sao cho M là trung điểm của AP.
Xét \(\Delta AMC\) và \(\Delta PMB\)có:
AM = PM
MC = MB
\(\widehat {AMC} = \widehat {PMB}\)
\( \Rightarrow \Delta AMC = \Delta PMB\left( {c – g – c} \right)\)
\( \Rightarrow \left\{ \begin{array}{l}AC = PB\\\widehat {MAC} = \widehat {MPB}\end{array} \right.\)
Do AB > AC suy ra AB > PB
Xét tam giác ABP có AB > PB
\(\begin{array}{l} \Rightarrow \widehat {MPB} > \widehat {MAB}\\ \Rightarrow \widehat {MAC} > \widehat {MAB}\end{array}\)
b)
Ta có: AD là tia phân giác của góc BAC nên \(\widehat {DAB} = \widehat {DAC} = \dfrac{{\widehat {BAC}}}{2} \Rightarrow \widehat {BAC} = 2\widehat {DAC}\)
Lại có:
\(\begin{array}{l}\widehat {MAC} > \widehat {MAB}\left( {cmt} \right)\\ \Rightarrow \widehat {MAC} + \widehat {MAC} > \widehat {MAB} + \widehat {MAC}\\ \Rightarrow 2\widehat {MAC} > \widehat {BAC}\\ \Rightarrow 2\widehat {MAC} > 2\widehat {DAC}\\ \Rightarrow \widehat {MAC} > \widehat {DAC}\end{array}\)
Vậy D thuộc đoạn thẳng MC.
–>
— *****
