Giải bài 9.10 trang 52 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Cho tam giác có độ dài cạnh lớn nhất bằng 4 cm. Hãy giải thích tại sao chu vi tam giác đó bé hơn 12 cm và lớn hơn 8 cm.
Phương pháp giải:
-Chu vi tam giác bằng tổng ba cạnh.
-Áp dụng bất đẳng thức tam giác.
Lời giải chi tiết:
Gọi độ dài ba cạnh tam giác là a, b, c (cm), (a < b < c)
Cạnh lớn nhất là a = 4, b < 4, c < 4
Chu vi tam giác là: a + b + c < 4 + 4 + 4 =12
Mặt khác, theo bất đẳng thức tam giác:
b + c > a
=>a + b + c > a + a
=>a + b + c > 2a = 8
Vậy 8 < a + b + c < 12 hay chu vi tam giác đó bé hơn 12 cm và lớn hơn 8 cm.
–>
— *****
Giải bài 9.11 trang 52 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Tam giác ABC có AB = 2cm, BC = 5cm, AC = b (cm) với b là một số nguyên. Hỏi b có thể bằng bao nhiêu?
Phương pháp giải:
Áp dụng bất đẳng thức tam giác trong tam giác ABC: BC – AB < AC < BC + AB.
Lời giải chi tiết:
Ta có: AC = b (cm)
Áp dụng bất đẳng thức cho tam giác ABC, có:
BC – AB < AC < BC + AB
=>5 – 2 < b < 5 + 2
=>3 < b < 7
Mà b nguyên nên b = {4; 5; 6}
–>
— *****
Giải bài 9.12 trang 52 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Tam giác ABC có AB = 2cm, BC = 3cm. Đặt CA = b (cm)
a)Chứng minh rằng 1 < b < 5
b) Giả sử rằng với 1 < b < 5, có tam giác ABC thoả mãn AB = 2cm, BC = 3 cm, CA = b (cm). Với mỗi tam giác đó, hãy sắp xếp ba góc A, B, C theo thứ tự từ bé đến lớn.
Phương pháp giải:
a)Áp dụng: BC – AB < CA < BC + AB
b)Áp dụng mối liên hệ giữa cạnh và góc trong tam giác.
Chia 3 trường hợp: \(1 < b \le 2\); \(2 < b \le 3\);\(3 < b < 5\).
Lời giải chi tiết:
a)
Áp dụng bất đẳng thức tam giác cho tam giác ABC:
BC – AB < CA < BC + AB
=>3 – 2 < b < 3 + 2
=>1 < b < 5 (đpcm)
b)
AB = 2 cm, BC = 3 cm, AC = b
Với \(1 < b \le 2\) \( \Rightarrow b \le AB < BC \Rightarrow \widehat B \le \widehat C < \widehat A\)(Mối liên hệ giữa cạnh và góc trong tam giác)
Với \(2 < b \le 3 \Rightarrow AB < CA \le BC \Rightarrow \widehat C < \widehat B \le \widehat A\)
Với \(3 < b < 5 \Rightarrow AB < BC < CA \Rightarrow \widehat C < \widehat A < \widehat B\)
–>
— *****
Giải bài 9.13 trang 52 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
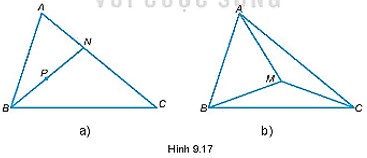
a) Cho P là một điểm bên trong tam giác ABC. Chứng minh rằng:
AB + AC > PB + PC
b) Cho M là một điểm bên trong tam giác ABC. Chứng minh rằng:
\(\dfrac{1}{2}\left( {AB + BC + CA} \right) < MA + MB + MC < AB + BC + CA\)
Phương pháp giải:
a)
– AB + AC = AB + AN + NC = (AB + AN) + NC
-Áp dụng các bất đẳng thức tam giác: tam giác ABN, tam giác PNC.
b)
-Chứng minh: \(MA + MB + MC > \dfrac{{AB + BC + CA}}{2}\)(áp dụng bđt tam giác ABM, MBC, MAC)
-Chứng minh:
M là điểm nằm trong tam giác ABC:
AB + AC > MB + MC
CA + CB > MA + MB
BA + BC > MA + MC
Lời giải chi tiết:

a)
P là điểm nằm trong tam giác ABC, đường thẳng BP cắt cạnh AC tại N
Ta có:
AB + AC = AB + AN + NC = (AB + AN) + NC (1)
Xét tam giác ABN: AB + AN > BN (Bất đẳng thức tam giác)
=>AB + AN > BP + PN (2)
Từ (1) và (2) suy ra: AB + AC > BP + (PN + NC) > BP + PC (Bất đẳng thức tam giác PNC)
b)
Ta có:
MA + MB > AB (bất đẳng thức trong tam giác ABM)
MB + MC > BC (bất đẳng thức trong tam giác MBC)
MC + MA > CA (bất đẳng thức trong tam giác MAC)
Cộng vế trái với vế trái, vế phải với vế phải:
2(MA + MB + MC) > AB + BC + CA
\( \Rightarrow MA + MB + MC > \dfrac{{AB + BC + CA}}{2}\) (1)
Mặt khác theo a)
M là điểm nằm trong tam giác ABC:
AB + AC > MB + MC
CA + CB > MA + MB
BA + BC > MA + MC
Cộng VT với VT, VP với VP:
2(AB + BC + CA) > 2(MA + MB + MC)
=>AB + BC + CA > MA + MB + MC (2)
Từ (1) và (2) suy ra:
\(\dfrac{1}{2}\left( {AB + BC + CA} \right) < MA + MB + MC < AB + BC + CA\)
–>
— *****
