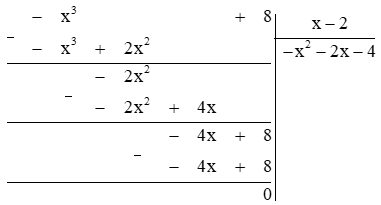
GIẢI CHI TIẾT Giải SBT bài cuối chương VI trang 68 – Chương 6 SBT Toán 7 Cánh diều
================
Giải bài 50 trang 55 SBT Toán 7 Cánh diều tập 2 – CD
Giá trị của biểu thức (x2 – 8)(x + 3) – (x – 2)(x + 5) tại x = 3 là:
A. -2 B. 16
C. -10 D. 10
Phương pháp giải
Bước 1: Rút gọn biểu thức
Bước 2: Thay x = 3 vào biểu thức để tính giá trị
Lời giải chi tiết
Ta có: (x2 – 8)(x + 3) – (x – 2)(x + 5) = \({x^3} + 3{x^2} – 8x – 24 – ({x^2} + 5x – 2x – 10)\)
\( = {x^3} + 3{x^2} – 8x – 24 – {x^2} – 5x + 2x + 10\)
\( = {x^3} + 2{x^2} – 11x – 14\)
Giá trị biểu thức tại x = 3 là: \({3^3} + {2.3^2} – 11.3 – 14 = 27 + 18 – 33 – 14 = – 2\)
Chọn A
Giải bài tập Toán 7 Cánh diều Bài tập cuối chương 6
Giải bài 51 trang 55 SBT Toán 7 Cánh diều tập 2 – CD
Biểu thức nào sau đây là đa thức một biến? Tìm biến và bậc của đa thức đó.
a) -2 022x
b) – 6x2 – 4x + 2
c) 3un – 8u2 – 20 \((n \in \mathbb{N},n > 2)\)
d) \(\frac{1}{x} + {x^3} – 2{x^2} + 1\)
Phương pháp giải
Bước 1: Xác định đa thức một biến (chỉ có một ẩn duy nhất)
Bước 2: Tìm biến và bậc là hệ số của lũy thừa cao nhất của biến
Lời giải chi tiết
a) Biểu thức -2 022x là đa thức một biến x có bậc là 1
b) Biểu thức – 6x2 – 4x + 2 là đa thức một biến x có bậc là 2
c) Biểu thức 3un – 8u2 – 20 \((n \in \mathbb{N},n > 2)\) là đa thức một biến u có bậc là n
d) Biểu thức \(\frac{1}{x} + {x^3} – 2{x^2} + 1\) không là đa thức một biến
Giải bài tập Toán 7 Cánh diều Bài tập cuối chương 6
Giải bài 52 trang 55 SBT Toán 7 Cánh diều tập 2 – CD
Tính giá trị của biểu thức:
a) A = 56 – 5a + 6b tại a = 22, b = 23
b) B = 6xyz – 3xy – 19z tại x = 11, y = 32, z = 0
c) C = x2021y – 2 022x2 +2 023y3 + 7 tại x = −1 và y = 1
d) \(D = {x^4} – 17{x^3} + 17{x^2} – 17x + 21\) tại x = 16
Phương pháp giải
Thay các giá trị ẩn tương ứng vào từng biểu thức và tính giá trị các biểu thức đó
Lời giải chi tiết
a) Thay a = 22, b = 23 vào biểu thức A ta có: \(A = 56 – 5.22 + 6.23 = 56 – 110 + 138 = 84\)
b) Thay x = 11, y = 32, z = 0 vào biểu thức B ta có: \(B = 6.11.32.0 – 3.11.32 – 19.0 = – 1056\)
c) Thay x = −1 và y = 1 vào biểu thức C ta có:
\(C = {( – 1)^{2021}}.1 – 2022.{( – 1)^2} + {2023.1^3} + 7 = – 1 – 2022 + 2023 + 7 = 7\)
d) Thay x = 16 vào biểu thức D ta có:
\(D = {16^4} – {17.16^3} + {17.16^2} – 17.16 + 21 = 65536 – 69632 + 4352 – 272 + 21 = 5\)
Giải bài tập Toán 7 Cánh diều Bài tập cuối chương 6
Giải bài 53 trang 55 SBT Toán 7 Cánh diều tập 2 – CD
Một bể đang chứa 500 1 nước. Người ta mở một vòi nước cho chảy vào bể đó, mỗi phút vòi nước đó chảy vào bể được 50 1 nước. Viết biểu thức biểu thị lượng nước có trong bể sau khi đã mở vòi nước đó được x phút, biết rằng sau 1 phút bể nước đó chưa đầy.
Phương pháp giải
Bước 1: Từ giả thiết biểu diễn lượng nước chảy vào bể trong x phút
Bước 2: Tính tổng lượng nước có trong bể (tổng lượng nước thêm và lượng nước ban đầu)
Lời giải chi tiết
Theo bài ra, 1 phút vòi nước chảy vào bể được 50 l nước
Suy ra trong x phút vòi nước chảy vào bể được 50x l nước
Vậy lượng nước có trong bể sau x phút là: 500 + 50x (l) nước
Giải bài tập Toán 7 Cánh diều Bài tập cuối chương 6
Giải bài 54 trang 55 SBT Toán 7 Cánh diều tập 2 – CD
Viết đa thức biến x trong mỗi trường hợp sau:
a) Đa thức bậc nhất có hệ số của biến bằng – 7 và hệ số tự do bằng 0
b) Đa thức bậc ba có hệ số của luỹ thừa bậc hai và bậc nhất của biến đều bằng 5
c) Đa thức bậc bốn có tổng hệ số của luỹ thừa bậc ba và bậc hai của biến bằng 6 và hệ số tự do bằng − 1
d) Đa thức bậc tám trong đó tất cả các hệ số của luỹ thửa bậc lẻ của biến đều bằng 0
Phương pháp giải
Bước 1: Xác định dạng của các đa thức
+ Bậc nhất: \(ax + b\)
+ Bậc hai: \(a{x^3} + b{x^2} + cx + d\)
+ Bậc bốn: \(a{x^4} + b{x^3} + c{x^2} + dx + e\)
+ Bậc tám: \(a{x^8} + b{x^7} + c{x^6} + d{x^5} + e{x^4} + m{x^3} + n{x^2} + px + q\)
Bước 2: Tìm các hệ số tương ứng của từng đa thức theo giả thiết (hệ số nào không có điều kiện thì giữ nguyên dạng biến)
Lời giải chi tiết
a) Đa thức bậc nhất có hệ số của biến bằng -7 và hệ số tự do bằng 0 có dạng: \( – 7x\)
b) Đa thức bậc ba có hệ số của luỹ thừa bậc hai và bậc nhất của biến đều bằng 5 có dạng:
\(a{x^3} + 5{x^2} + 5x + d\) (với a, d là các số cho trước và a ≠ 0)
c) Đa thức bậc bốn có tổng hệ số của luỹ thừa bậc ba và bậc hai của biến bằng 6 và hệ số tự do bằng – 1
có dạng: \(a{x^4} + b{x^3} + c{x^2} + dx + e\)
Khi đó: \(b + c = 6 \Rightarrow c = 6 – b\)
Vậy đa thức cần tìm là: \(a{x^4} + b{x^3} + (6 – b){x^2} + dx – 1\) (với a, b, d là các số cho trước và a ≠ 0)
d) Đa thức bậc tám trong đó tất cả các hệ số của luỹ thửa bậc lẻ của biến đều bằng 0 có dạng:
\(a{x^8} + b{x^6} + c{x^4} + d{x^2} + e\) (với a, b, c, d, e là các số cho trước và a ≠ 0)
Giải bài tập Toán 7 Cánh diều Bài tập cuối chương 6
Giải bài 55 trang 55 SBT Toán 7 Cánh diều tập 2 – CD
Tìm giá trị của m để đa thức sau là đa thức bậc ba theo biến x: \(P(x) = ({m^2} – 25){x^4} + (20 + 4m){x^3} + 17{x^2} – 23\)
Phương pháp giải
Bước 1: Xác định dạng của đa thức bậc ba biến x: \(a{x^3} + b{x^2} + cx + d\) (a ≠ 0). Khi đó lũy thừa bậc cao nhất của x là x3
Bước 2: Xác định m để hệ số x4 bằng 0 và hệ số x3 khác 0
Lời giải chi tiết
Ta có: \(P(x) = ({m^2} – 25){x^4} + (20 + 4m){x^3} + 17{x^2} – 23\) là đa thức bậc ba biến x khi và chỉ khi:
\({m^2} – 25 = 0\) và \(20 + 4m \ne 0\)
Ta có: \({m^2} – 25 = 0\)\( \Rightarrow {m^2} = 25 \Rightarrow m = \pm 5\)
+ Với m = 5 thì 20 + 4m = 20 + 4.5 = 40 ≠ 0 ® m = 5 thỏa mãn
+ Với m = -5 thì 20 + 4m = 20 + 4.(-5) = 20 – 20 = 0 ® m = -5 không thỏa mãn
Vậy \(m = 5\) thỏa mãn đề bài
Giải bài tập Toán 7 Cánh diều Bài tập cuối chương 6
Giải bài 56 trang 55 SBT Toán 7 Cánh diều tập 2 – CD
Cho đa thức \(A(x) = – 11{x^5} + 4{x^3} – 12{x^2} + 11{x^5} + 13{x^2} – 7x + 2\)
a) Thu gọn và sắp xếp đa thức A(x) theo số mũ giảm dần của biến
b) Tìm bậc của đa thức A(x)
c) Tính giá trị của đa thức A(x) tại x = −1; x = 0; x = 2
Phương pháp giải
Bước 1: Cộng, trừ các đơn thức có cùng số mũ của biến để rút gọn và sắp xếp đa thức rút gọn theo số mũ giảm dần của biến
Bước 2: Tìm bậc của đa thức là số mũ cao nhất của biến
Bước 3: Thay x = -1, x = 0, x = 2 vào đa thức rút gọn để tính giá trị A(−1), A(0), A(2)
Lời giải chi tiết
a) \(A(x) = – 11{x^5} + 4{x^3} – 12{x^2} + 11{x^5} + 13{x^2} – 7x + 2 = 4{x^3} + {x^2} – 7x + 2\)
b) Bậc của đa thức A(x) là 3
c) Ta có:
\(A( – 1) = 4.{( – 1)^3} + {( – 1)^2} – 7.( – 1) + 2 = – 4 + 1 + 7 + 2 = 6\)
\(A(0) = {4.0^3} + {0^2} – 7.0 + 2 = 2\)
\(A(2) = {4.2^3} + {2^2} – 7.2 + 2 = 32 + 4 – 14 + 2 = 24\)
Giải bài tập Toán 7 Cánh diều Bài tập cuối chương 6
Giải bài 57 trang 56 SBT Toán 7 Cánh diều tập 2 – CD
Tính:
a) \(( – 4{x^3} – 13{x^2} + 2{x^5}) + (13{x^2} + 2{x^3} – 12x – 1)\)
b) \((12{x^6} – 11{x^2} + 3{x^3} + 9) – (13{x^5} + 2{x^3} – 11{x^2} – 11x)\)
c) \((8{x^3} – {x^2} + 1)({x^2} – 1)\)
d) \((8{x^3} + 6{x^2} + 3x + 1):(2x + 1)\)
Phương pháp giải
Thực hiện các phép toán cộng/trừ/nhân/chia đa thức theo quy tắc để rút gọn các biểu thức trên
Lời giải chi tiết
a) \(( – 4{x^3} – 13{x^2} + 2{x^5}) + (13{x^2} + 2{x^3} – 12x – 1)\)\( = – 4{x^3} – 13{x^2} + 2{x^5} + 13{x^2} + 2{x^3} – 12x – 1\)
\( = 2{x^5} – 2{x^3} – 12x – 1\)
b) \((12{x^6} – 11{x^2} + 3{x^3} + 9) – (13{x^6} + 2{x^3} – 11{x^2} – 11x)\)\( = 12{x^6} – 11{x^2} + 3{x^3} + 9 – 13{x^6} – 2{x^3} + 11{x^2} + 11x\)
\( = – {x^6} + {x^3} + 11x + 9\)
c) \((8{x^3} – {x^2} + 1)({x^2} – 1) = 8{x^5} – 8{x^3} – {x^4} + {x^2} + {x^2} – 1 = 8{x^5} – {x^4} – 8{x^3} + 2{x^2} – 1\)
d) \((8{x^3} + 6{x^2} + 3x + 1):(2x + 1)\)
Vậy \((8{x^3} + 6{x^2} + 3x + 1):(2x + 1) = 4{x^2} + x + 1\)
Giải bài tập Toán 7 Cánh diều Bài tập cuối chương 6
Giải bài 58 trang 56 SBT Toán 7 Cánh diều tập 2 – CD
Tìm đa thức C(x) sao cho A(x) – C(x) = B(x), biết:
a) \(A(x) = {x^3} + {x^2} + x – 2,B(x) = 9 – 2x + 11{x^3} + {x^4}\)
b) \(A(x) = – 12{x^5} + 2{x^3} – 2,B(x) = 9 – 2x – 11{x^2} + 2{x^3} – 11{x^5}\)
Phương pháp giải
Thực hiện phép trừ hai đa thức một biến theo quy tắc với \(C(x) = A(x) – B(x)\)
Lời giải chi tiết
a) \(C(x) = A(x) – B(x)\)\( = ({x^3} + {x^2} + x – 2) – (9 – 2x + 11{x^3} + {x^4})\)\( = {x^3} + {x^2} + x – 2 – 9 + 2x – 11{x^3} – {x^4}\)
\( = – {x^4} – 10{x^3} + {x^2} + 3x – 11\)
Vậy \(C(x) = – {x^4} – 10{x^3} + {x^2} + 3x – 11\)
b) \(C(x) = A(x) – B(x)\)\( = ( – 12{x^5} + 2{x^3} – 2) – (9 – 2x – 11{x^2} + 2{x^3} – 11{x^5})\)
\( = – 12{x^5} + 2{x^3} – 2 – 9 + 2x + 11{x^2} – 2{x^3} + 11{x^5}\)
\( = – {x^5} + 11{x^2} + 2x – 11\)
Vậy \(C(x) = – {x^5} + 11{x^2} + 2x – 11\)
Giải bài tập Toán 7 Cánh diều Bài tập cuối chương 6
Giải bài 59 trang 56 SBT Toán 7 Cánh diều tập 2 – CD
Tìm đa thức Q(x) sao cho P(x) . Q(x) = R(x), biết:
a) \(P(x) = x – 2,R(x) = – {x^3} + 8\)
b) \(P(x) = {x^2} – 3x + 2,R(x) = 10 – 13x + 2{x^2} + {x^3}\)
Phương pháp giải
Thực hiện phép chia hai đa thức một biến theo quy tắc với \(Q(x) = R(x):P(x)\)
Lời giải chi tiết
Ta có: P(x) . Q(x) = R(x) \( \Rightarrow Q(x) = R(x):P(x)\)
a) \(Q(x) = R(x):P(x)\)\( = ( – {x^3} + 8):(x – 2)\)
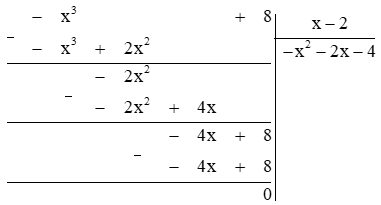
Vậy \(Q(x) = – {x^2} – 2x – 4\)
b) \(Q(x) = R(x):P(x)\)\( = (10 – 13x + 2{x^2} + {x^3}):({x^2} – 3x + 2)\)\( = ({x^3} + 2{x^2} – 13x + 10):({x^2} – 3x + 2)\)
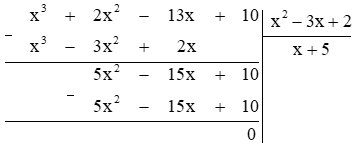
Vậy \(Q(x) = x + 5\)
Giải bài tập Toán 7 Cánh diều Bài tập cuối chương 6
Giải bài 60 trang 56 SBT Toán 7 Cánh diều tập 2 – CD
Tìm hệ số a sao cho đa thức \(G(x) = {x^4} + {x^2} + a\) chia hết cho đa thức \(M(x) = {x^2} – x + 1\)
Phương pháp giải
Bước 1: Đặt tính rồi thực hiện phép chia đến khi tìm được số dư chứa số a
Bước 2: Tìm a để số dư bằng 0 rồi kết luận
Lời giải chi tiết
Xét \(G(x):M(x) = ({x^4} + {x^2} + a):({x^2} – x + 1)\)
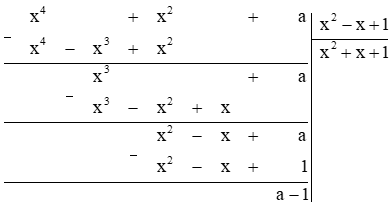
\( \Rightarrow \) Số dư trong phép chia \(G(x):M(x) = ({x^4} + {x^2} + a):({x^2} – x + 1)\)là a – 1
Để G(x) chia hết cho M(x) thì a – 1 = 0 \( \Rightarrow \) a = 1
Giải bài tập Toán 7 Cánh diều Bài tập cuối chương 6
Giải bài 61 trang 56 SBT Toán 7 Cánh diều tập 2 – CD
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) x = 2 và x = -3 là nghiệm của đa thức \(P(x) = {x^2} – 5x + 6\)
b) Đa thức bậc bốn luôn có nhiều hơn bốn nghiệm
c) Mỗi phần tử của tập hợp {0; 1; –1} là nghiệm của đa thức \(P(x) = {x^3} – x\)
Phương pháp giải
Thay các giá trị x vào đa thức P(x) rồi kết luận nghiệm của P(x)
Lưu ý: Đa thức có bậc n luôn có nhiều nhất n nghiệm
Lời giải chi tiết
a) Ta có:
\(P(2) = {2^2} – 5.2 + 6 = 4 – 10 + 6 = 0 \Rightarrow x = 2\) là nghiệm của P(x)
\(P( – 3) = {( – 3)^2} – 5.( – 3) + 6 = 9 + 15 + 6 = 30 \ne 0 \Rightarrow x = – 3\) không là nghiệm của P(x)
Phát biểu a) sai
b) Vì đa thức có bậc n (\(n \in \mathbb{N},n \ge 1\)) luôn có nhiều nhất n nghiệm nên đa thức bậc bốn có không quá 4 nghiệm
Phát biểu b) sai
c) Ta có:
\(P(0) = {0^3} – 0 = 0 \Rightarrow x = 0\) là nghiệm của P(x)
\(P(1) = {1^3} – 1 = 1 – 1 = 0 \Rightarrow x = 1\) là nghiệm của P(x)
\(P( – 1) = {( – 1)^3} – ( – 1) = – 1 + 1 = 0 \Rightarrow x = – 1\) là nghiệm của P(x)
Phát biểu c) đúng
Giải bài tập Toán 7 Cánh diều Bài tập cuối chương 6
Giải bài 62 trang 56 SBT Toán 7 Cánh diều tập 2 – CD
Cho đa thức \(P(x) = a{x^4} + b{x^3} + c{x^2} + dx + e\) (a ≠ 0) với \(a + b + c + d + e = 0\). Chứng tỏ rằng x = 1 là nghiệm của đa thức P(x)
Phương pháp giải
Tính P(1) và sử dụng giả thiết \(a + b + c + d + e = 0\) rồi kết luận
Lời giải chi tiết
Ta có: \(P(1) = a{.1^4} + b{.1^3} + c{.1^2} + d.1 + e = a + b + c + d + e\) = 0
Vậy x = 1 là nghiệm của đa thức P(x)
Giải bài tập Toán 7 Cánh diều Bài tập cuối chương 6
Giải bài 63 trang 56 SBT Toán 7 Cánh diều tập 2 – CD
Cho đa thức \(Q(x) = a{x^2} + bx + c\)(a ≠ 0). Chứng minh rằng nếu Q(x) nhận 1 và –1 là nghiệm thì a và c là hai số đối nhau
Phương pháp giải
Bước 1: Tính Q(1) và Q(-1) và cho hai biểu thức bằng 0
Bước 2: Xét \(Q(1) = Q( – 1)\) và tìm mối liên hệ giữa a và c
Lời giải chi tiết
Vì 1 là nghiệm của Q(x) nên \(Q(1) = a{.1^2} + b.1 + c = a + b + c = 0\)
Vì –1 là nghiệm của Q(x) nên \(Q( – 1) = a.{( – 1)^2} + b.( – 1) + c = a – b + c = 0\)
Khi đó \(Q(1) = Q( – 1) \Rightarrow a + b + c = a – b + c\)\( \Rightarrow b + b = 0 \Rightarrow b = 0\)
Với b = 0 thì \(a + c = 0 \Rightarrow a = – c\) (ĐPCM)
Giải bài tập Toán 7 Cánh diều Bài tập cuối chương 6
Giải bài 64 trang 56 SBT Toán 7 Cánh diều tập 2 – CD
Một cửa hàng bán hoa sau khi tăng giá 50 nghìn đồng mỗi chậu hoa so với giá bán ban đầu là 3x (nghìn đồng) thì số tiền thu được là 3x2 + 53x + 50 (nghìn đồng). Tính số chậu hoa mà cửa hàng đã bán theo x
Phương pháp giải
Bước 1: Tính giá bán hoa sau khi tăng theo x (thu được đa thức biến x)
Bước 2: Thực hiện phép chia số chậu hoa bán được = (số tiền thu được) : (giá bán 1 chậu hoa)
Lời giải chi tiết
Theo đề bài, giá bán một chậu hoa sau khi tăng giá là: \(3x + 50\)(nghìn đồng)
Gọi P(x) là biểu thức biểu thị số chậu hoa bán được. Khi đó: \(P(x) = (3{x^2} + 53x + 50):(3x + 50)\)
\( \Rightarrow P(x) = x + 1\)
Vậy số chậu hoa mà cửa hàng đã bán là: x + 1 (chậu)
Giải bài tập Toán 7 Cánh diều Bài tập cuối chương 6
Giải bài 65 trang 56 SBT Toán 7 Cánh diều tập 2 – CD
Tháng 5 năm 2019, nhiều đại biểu trên cả nước đã “hội quân” trên một tàu kiểm ngư rời cảng biển quốc tế Cam Ranh để bắt đầu hải trình nối tình yêu đất liền với biển đảo Trường Sa. Do thời tiết xấu, tàu kiểm ngư đã giảm 15
a) 1 giờ
b) 4 giờ
c) y giờ
Phương pháp giải
Bước 1: Tính tốc độ của tàu sau khi giảm theo x
Bước 2: Tính quãng đường (đơn vị hải lí) mà tàu đi được với từng thời gian cho trước (S = v.t)
Lời giải chi tiết
Theo đề bài, tốc độ của tàu kiểm ngư sau khi giảm 15
a) Số hải lí mà tàu kiểm ngư đã đi trong 1 giờ là: \(0,85x.1 = 0,85x\) (hải lí)
b) Số hải lí mà tàu kiểm ngư đã đi trong 4 giờ là: \(0,85x.4 = 3,4x\) (hải lí)
c) Số hải lí mà tàu kiểm ngư đã đi trong y giờ là: \(0,85x.y = 0,85xy\) (hải lí)
Giải bài tập Toán 7 Cánh diều Bài tập cuối chương 6
Giải bài 66 trang 57 SBT Toán 7 Cánh diều tập 2 – CD
Lượng khí thải gây hiệu ứng nhà kính do các hoạt động của con người là nguyên nhân gây ra nhiệt độ Trái Đất tăng một cách đáng kể. Các nhà khoa học đưa ra biểu thức dự báo nhiệt độ trung bình trên bề mặt Trái Đất như sau: T = 0,02x + 15. Trong đó, T là nhiệt độ trung bình của bề mặt Trái Đất tính theo độ C, x là số năm kể từ năm 1960. Tính nhiệt độ trung bình của bề mặt Trái Đất vào các năm 1965 và năm 2023 theo biểu thức dự báo trên
Phương pháp giải
Bước 1: Xác định số năm trong từng mốc thời gian 1965 và 2023
Bước 2: Thay các giá trị vừa tìm được vào biểu thức T và tính giá trị rồi kết luận
Lời giải chi tiết
a) Số năm kể từ năm 1960 đến năm 1965 là 5 năm
Với x = 5 thì biểu thức T có giá trị là: \(T = 0,02.5 + 15 = 0,1 + 15 = 15,1\) (0C)
Vậy nhiệt độ trung bình của bề mặt Trái Đất vào năm 1965 là 15,1 0C
b) Số năm kể từ năm 1960 đến năm 2023 là 63 năm
Với x = 63 thì biểu thức T có giá trị là: \(T = 0,02.63 + 15 = 1,26 + 15 = 16,26\) (0C)
Vậy nhiệt độ trung bình của bề mặt Trái Đất vào năm 1965 là 16,26 0C
Giải bài tập Toán 7 Cánh diều Bài tập cuối chương 6
Giải bài 67 trang 57 SBT Toán 7 Cánh diều tập 2 – CD
Giá bán lẻ 1 hộp sữa là 7 000 đồng, giá cho 1 lốc sữa 4 hộp là 26 000 đồng. Nếu mua từ 4 lốc sữa trở lên thì cứ 2 lốc sữa được tặng 1 hộp. Vậy nếu bác Hoa mua 2a \((a \in \mathbb{N},2 \le a < 10)\) lốc sữa thì sẽ tiết kiệm bao nhiêu tiền so với mua lẻ từng hộp?
Phương pháp giải
Bước 1: Xác định số hộp sữa được tặng khi mua 2a lốc sữa
Bước 2: Xác định số tiền mua 2a lốc sữa và tổng số hộp sữa có được
Bước 3: Tính số tiền cần trả khi mua lẻ số hộp sữa tìm được ở bước 2
Bước 4: Tìm số tiền tiết kiệm được bằng hiệu số tiền mua lẻ và số tiền mua 2a lốc sữa đã tìm được ở bước trên
Lời giải chi tiết
Theo đề bài, nếu mua từ 4 lốc sữa trở lên thì cứ 2 lốc sữa được tặng 1 hộp. Do đó nếu mua 2a lốc sữa được tặng a hộp sữa
Số tiền bác Hoa cần trả khi mua 2a lốc sữa là: \(2a.26000 = 52000a\) (đồng)
Tổng số hộp sữa bác Hoa có được là: \(2a.4 + a = 8a + a = 9a\) (hộp)
Số tiền bác Hoa cần trả khi mua lẻ 9a hộp sữa là: \(9a.7000 = 63000a\) (đồng)
Vậy số tiền bác Hoa tiết kiệm được là: \(63000a – 52000a = 11000a\) (đồng)
Giải bài tập Toán 7 Cánh diều Bài tập cuối chương 6
Giải bài 68 trang 57 SBT Toán 7 Cánh diều tập 2 – CD
Nhân dịp cuối năm, một cửa hàng cần thanh lí một lô hàng (gồm 100 sản phẩm cùng loại) với giá bán là x đồng/chiếc. Lần đầu cửa hàng giảm 10
Phương pháp giải
Bước 1: Tính giá bán khi giảm 10
Bước 2: Tính tổng số tiền cửa hàng thu được khi bán 2 lần
Lời giải chi tiết
+ Giá bán 1 sản phẩm khi cửa hàng giảm 10
Số tiền cửa hàng thu được khi bán 15 sản phẩm lần đầu là: \(15.0,9x = 13,5x\) (đồng)
+ Giá bán 1 sản phẩm khi cửa hàng giảm 5
\(0,9x – 0,9x.5% = 0,9x – 0,045x = 0,855x\) (đồng)
Số tiền cửa hàng thu được khi bán 85 sản phẩm còn lại là: \(85.0,855x = 72,675x\) (đồng)
Vậy tổng số tiền cửa hàng thu được khi bán 100 sản phẩm là:
\(13,5x + 72,675x = 86,175x\) (đồng)
Giải bài tập Toán 7 Cánh diều Bài tập cuối chương 6
Giải bài 69 trang 57 SBT Toán 7 Cánh diều tập 2 – CD
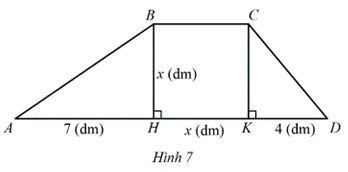
Tính diện tích của hình thang ABCD với các số đo cho như Hình 7 theo x.
Phương pháp giải
Bước 1: Xác định chiều cao, đáy lớn và đáy nhỏ của hình thang theo x
Bước 2: Áp dụng công thức tính diện tích hình thang ABCD
Lời giải chi tiết
Từ hình vẽ hình thang ABCD có:
+ đáy nhỏ BC = HK = x (dm)
+ đáy lớn AD = AH + HK + KD = 7 + x + 4 = x + 11 (dm)
+ chiều cao BH = x (dm)
Diện tích hình thang ABCD là:
\({S_{ABCD}} = \frac{1}{2}.BH.(BC + AD) = \frac{1}{2}.x.(x + x + 11) = \frac{1}{2}x(2x + 11)\)\( = \frac{1}{2}(2{x^2} + 11x) = {x^2} + \frac{{11}}{2}x\) (dm2)
Giải bài tập Toán 7 Cánh diều Bài tập cuối chương 6
=============
