GIẢI CHI TIẾT Giải SBT Bài 19 Chương 7 – SBT Toán 10 KNTT
============
Giải bài 7.1 trang 31 SBT Toán 10 Kết nối tri thức tập 2 – KNTT
Trong mặt phẳng \(Oxy\), cho điểm \(D\left( {0;2} \right)\) và hai vector \(\overrightarrow n = \left( {1; – 3} \right),\overrightarrow u = \left( {1;3} \right)\)
a) Viết phương trình tổng quát của đường thẳng d đi qua D và nhận \(\overrightarrow n \) là một vector pháp tuyến.
b) Viết phương trình tổng quát của đường thẳng \(\Delta \) đi qua D và nhận \(\overrightarrow u \) là một vector chỉ phương
Phương pháp giải
+ Phương trình tổng quát đường thẳng đi qua \(M\left( {{x_1},{y_1}} \right)\) nhận \(\overrightarrow {{a_1}} = \left( {a;b} \right)\) là vector pháp tuyến là: \(a\left( {x – {x_1}} \right) + b\left( {y – {y_1}} \right) = 0\)
+ \(\overrightarrow {{a_2}} = \left( {c;d} \right)\) là vector chỉ phương à \(\overrightarrow {{a_3}} = \left( {d; – c} \right)\)là vector pháp tuyến của đường thẳng đó
Lời giải chi tiết
a) Phương trình tổng quát đường thẳng đi qua \(D\left( {0;2} \right)\) nhận \(\overrightarrow n = \left( {1; – 3} \right)\) là vector pháp tuyến là: \(1\left( {x – 0} \right) – 3\left( {y – 2} \right) = 0 \Rightarrow d:x – 3y + 6 = 0\)
b) Đường thẳng \(\Delta \) nhận \(\overrightarrow u = \left( {1;3} \right)\) là vector chỉ phương à đường thẳng có \(\overrightarrow {{u_1}} = \left( {3; – 1} \right)\) là vector pháp tuyến
Phương trình tổng quát đường thẳng đi qua \(D\left( {0;2} \right)\) nhận \(\overrightarrow {{u_1}} = \left( {3; – 1} \right)\) là vector pháp tuyến là: \(3\left( {x – 0} \right) – 1\left( {y – 2} \right) = 0 \Rightarrow \Delta :3x – y + 2 = 0\)
GIẢI SBT Toán 10 Kết nối tri thức Chương 7 Bài 19
Giải bài 7.2 trang 31 SBT Toán 10 Kết nối tri thức tập 2 – KNTT
Trong mặt phẳng \(Oxy\), cho ba điểm \(A\left( {1;2} \right);B\left( {0; – 1} \right)\) và \(C\left( { – 2;3} \right)\). Lập phương trình tổng quát của đường thẳng đi qua A và vuông góc với đường thẳng BC
Phương pháp giải
+ Phương trình tổng quát đường thẳng đi qua \(M\left( {{x_1},{y_1}} \right)\) nhận \(\overrightarrow {{a_1}} = \left( {a;b} \right)\) là vector pháp tuyến là: \(a\left( {x – {x_1}} \right) + b\left( {y – {y_1}} \right) = 0\)
Lời giải chi tiết
+ Phương trình đường thẳng đi qua A và vuông góc với BC tức là đường thẳng này có vector pháp tuyến là vector chỉ phương của đường thẳng BC
Tức là \(\overrightarrow n = \overrightarrow {BC} = \left( { – 2;4} \right) = – 2\left( {1; – 2} \right)\)
+ Viết phương trình đường thẳng biết đi qua điểm \(A\left( {1;2} \right)\) và có vector pháp tuyến \(\overrightarrow n = \left( {1; – 2} \right)\): \(1\left( {x – 1} \right) – 2\left( {y – 2} \right) = 0 \Rightarrow x – 2y + 3 = 0\)
GIẢI SBT Toán 10 Kết nối tri thức Chương 7 Bài 19
Giải bài 7.3 trang 31 SBT Toán 10 Kết nối tri thức tập 2 – KNTT
Trong mặt phẳng \(Oxy\), cho hai điểm \(A\left( {1;2} \right)\) và \(B\left( {2;3} \right)\). Tìm một vector chỉ phương của đường thẳng AB và viết phương trình tham số của đường thẳng AB
Phương pháp giải
Phương trình tham số của đường thẳng AB: đi qua \(A\left( {a,b} \right)\), nhận \(\overrightarrow {AB} = \left( {c,d} \right)\) là vector chỉ phương: \(\left\{ \begin{array}{l}x = a + ct\\y = b + dt\end{array} \right.\)
Lời giải chi tiết
+ Vector chỉ phương của đường thẳng AB là \(\overrightarrow {AB} = \left( {1;1} \right)\)
Phương trình tham số của đường thẳng AB: đi qua \(A\left( {1;2} \right)\), nhận \(\overrightarrow {AB} = \left( {1;1} \right)\) là vector chỉ phương: \(\left\{ \begin{array}{l}x = 1 + t\\y = 2 + t\end{array} \right.\)
GIẢI SBT Toán 10 Kết nối tri thức Chương 7 Bài 19
Giải bài 7.4 trang 31 SBT Toán 10 Kết nối tri thức tập 2 – KNTT
Trong mặt phẳng \(Oxy\), cho đường thẳng \(\Delta :2x – y + 5 = 0\). Tìm tất cả vector pháp tuyến có độ dài \(2\sqrt 5 \) của đường thẳng \(\Delta \)
Phương pháp giải
+ Vector pháp tuyến của đường thẳng tổng quát: \(ax + by + c = 0\) là \(\overrightarrow n = \left( {a;b} \right)\)
+ Độ dài vetor \(\overrightarrow n = \left( {a;b} \right)\) là \(\left| {\overrightarrow n } \right| = \sqrt {{a^2} + {b^2}} \)
Lời giải chi tiết
+ Vecto pháp tuyến của đường thẳng tổng quát: \(\Delta :2x – y + 5 = 0\) là \(\overrightarrow n = \left( {2t; – t} \right)\)
+ Độ dài vecto \(\overrightarrow n = \left( {2t; – t} \right)\) là \(\left| {\overrightarrow n } \right| = \sqrt {4{t^2} + {t^2}} = \sqrt {5{t^2}} = \left| t \right|\sqrt 5 = 2\sqrt 5 \Rightarrow \left| t \right| = 2 \Rightarrow t = \pm 2\)
Vậy các vecto phải tìm là \(\overrightarrow {{n_1}} = \left( {4; – 2} \right)\) và \(\overrightarrow {{n_2}} = \left( { – 4;2} \right)\)
GIẢI SBT Toán 10 Kết nối tri thức Chương 7 Bài 19
Giải bài 7.5 trang 31 SBT Toán 10 Kết nối tri thức tập 2 – KNTT
Trong mặt phẳng \(Oxy\), cho đường thẳng d có phương trình \(y = – 2x + 3\). Viết phương trình tham số và phương trình tổng quát của đường thẳng d
Phương pháp giải
+ Phương trình tổng quát đường thẳng đi qua \(M\left( {{x_1},{y_1}} \right)\) nhận \(\overrightarrow {{a_1}} = \left( {a;b} \right)\) là vecto pháp tuyến là: \(a\left( {x – {x_1}} \right) + b\left( {y – {y_1}} \right) = 0\)
+ Phương trình tham số của đường thẳng đi qua \(A\left( {a,b} \right)\), nhận \(\overrightarrow v = \left( {c,d} \right)\) là vecto chỉ phương: \(\left\{ \begin{array}{l}x = a + ct\\y = b + dt\end{array} \right.\)
Lời giải chi tiết
+ Phương trình \(y = – 2x + 3 \Rightarrow \) phương trình tổng quát \(2x + y – 3 = 0\)
+ Phương trình \(2x + y – 3 = 0\) có vetor pháp tuyến là \(\overrightarrow n = \left( {2;1} \right) \Rightarrow \overrightarrow v = \left( {1; – 2} \right)\) và đi qua điểm \(A\left( {0;3} \right)\) à phương trình tham số của đường thẳng d: \(\left\{ \begin{array}{l}x = t\\y = 3 – 2t\end{array} \right.\)
GIẢI SBT Toán 10 Kết nối tri thức Chương 7 Bài 19
Giải bài 7.6 trang 31 SBT Toán 10 Kết nối tri thức tập 2 – KNTT
Trong mặt phẳng \(Oxy\), cho điểm \(M\left( {2;1} \right)\) và đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 2 – t\\y = 2t\end{array} \right.\). Tìm điểm N thuộc đường thẳng \(\Delta \) sao cho \(MN = \sqrt 2 \)
Phương pháp giải
+ Độ dài đường thẳng MN có \(\overrightarrow {MN} = \left( {a;b} \right)\) là \(\left| {\overrightarrow {MN} } \right| = \sqrt {{a^2} + {b^2}} \)
Lời giải chi tiết
+ N thuộc đường thẳng \(\Delta \)\( \Rightarrow N\left( {2 – t;2t} \right)\)
+ \(\overrightarrow {MN} = \left( { – t;2t – 1} \right)\) có độ dài là \(\left| {\overrightarrow {MN} } \right| = \sqrt {{{\left( { – t} \right)}^2} + {{\left( {2t – 1} \right)}^2}} = \sqrt {5{t^2} – 4t + 1} = \sqrt 2 \)
\( \Rightarrow 5{t^2} – 4t + 1 = 2 \Rightarrow 5{t^2} – 4t – 1 = 0 \Rightarrow \left[ \begin{array}{l}t = 1\\t = \frac{{ – 1}}{5}\end{array} \right.\)
Vậy \(N\left( {1;2} \right)\) hoặc \(N\left( {\frac{{11}}{5};\frac{{ – 2}}{5}} \right)\)
GIẢI SBT Toán 10 Kết nối tri thức Chương 7 Bài 19
Giải bài 7.7 trang 31 SBT Toán 10 Kết nối tri thức tập 2 – KNTT
Trong mặt phẳng \(Oxy\), cho tam giác ABC có tọa độ ba đỉnh \(A\left( {0; – 1} \right);B\left( {2;3} \right)\) và \(C\left( { – 4;1} \right)\). Lập phương trình tham số của đường trung bình ứng với cạnh BC của tam giác ABC.
Phương pháp giải
+ Phương trình tham số của đường thẳng đi qua \(A\left( {a,b} \right)\), nhận \(\overrightarrow v = \left( {c,d} \right)\) là vecto chỉ phương: \(\left\{ \begin{array}{l}x = a + ct\\y = b + dt\end{array} \right.\)
Lời giải chi tiết
+ Đường trung bình ứng với cạnh BC là đường thẳng đi qua trung điểm của AB và AC => Đường thẳng này song song với đường thẳng BC => Vecto chỉ phương của đường thẳng này cùng phương với vecto chỉ phương của đường thẳng BC => \(\overrightarrow v = \overrightarrow {BC} = \left( { – 6; – 2} \right)\)
+ Viết phương trình tham số biết đường thẳng đi qua trung điểm của AB là \(M\left( {1;1} \right)\)và vetor chỉ phương \(\overrightarrow v = \left( {3;1} \right)\): \(\left\{ \begin{array}{l}x = 1 + 3t\\y = 1 + t\end{array} \right.\)
GIẢI SBT Toán 10 Kết nối tri thức Chương 7 Bài 19
Giải bài 7.8 trang 32 SBT Toán 10 Kết nối tri thức tập 2 – KNTT
Trong mặt phẳng \(Oxy\), cho hình vuông ABCD có \(A\left( { – 1;0} \right)\) và \(B\left( {1;2} \right)\)
a) Lập phương trình đường thẳng BC
b) Tìm tọa độ của điểm C biết rằng hoành hộ của điểm C là số dương
Phương pháp giải
+ Phương trình tổng quát đường thẳng đi qua \(M\left( {{x_1},{y_1}} \right)\) nhận \(\overrightarrow {{a_1}} = \left( {a;b} \right)\) là vecto pháp tuyến là: \(a\left( {x – {x_1}} \right) + b\left( {y – {y_1}} \right) = 0\)
Lời giải chi tiết
a) Phương trình đường thẳng BC đi qua \(B\left( {1;2} \right)\) và nhận \(\overrightarrow {AB} = \left( {2;2} \right) = 2\left( {1;1} \right)\) là vecto pháp tuyến
Phương trình tổng quát của BC: \(1\left( {x – 1} \right) + 1\left( {y – 2} \right) = 0 \Rightarrow x + y – 3 = 0\)
b) C thuộc đường thẳng BC \( \Rightarrow C\left( {t;3 – t} \right)\)
+ \(AB = \sqrt {{2^2} + {2^2}} = 2\sqrt 2 \)
+ \(\overrightarrow {BC} = \left( {t – 1;1 – t} \right) \Rightarrow BC = \sqrt {{{\left( {t – 1} \right)}^2} + {{\left( {1 – t} \right)}^2}} = \left| {t – 1} \right|\sqrt 2 \)
+ \(AB = BC \Rightarrow \left| {t – 1} \right|\sqrt 2 = 2\sqrt 2 \Rightarrow \left| {t – 1} \right| = 2 \Rightarrow \left[ \begin{array}{l}t = 3\\t = – 1\end{array} \right.\)
Với hoành độ của C là số dương => \(C\left( {3;0} \right)\)
GIẢI SBT Toán 10 Kết nối tri thức Chương 7 Bài 19
Giải bài 7.9 trang 32 SBT Toán 10 Kết nối tri thức tập 2 – KNTT
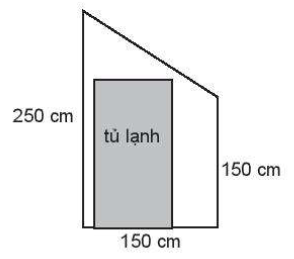
Nhà bạn Nam định đổi tủ lạnh và dự định kê vào vị trí dưới cầu thang. Biết vị trí kê tủ lạnh có mặt cát là một hình thang vuông với hai đáy lần lượt là 150 cm và 250 cm, chiều cao là 150 cm (như hình vẽ). Bố mẹ Nam định mua một tủ lạnh 2 cánh (Slide by slide) có chiều cao là 183 cm và bề ngang 90 cm. Bằng cách sử dụng tọa độ trong mặt phẳng, em hãy giúp Nam tính xem bố mẹ Nam có thể kê vừa chiếc tủ lạnh vào vị trí cần kê không?

Phương pháp giải
Gắn hệ trục tọa độ \(Oxy\), đặt vị trí các điểm nút.
Lời giải chi tiết
+ Gắn hệ trục tọa độ như hình vẽ:
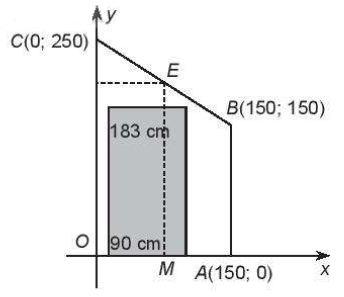
+ Để tận dung tối đa chiều cao thể khi kê tủ lạnh thì bố mẹ Nam sẽ kê tủ sát vào trục Oy, Do đó để kê được một chiếc tủ lạnh 2 cánh với bề ngang 90 cm thì chiều cao của tủ phải nhỏ hơn tung độ của điểm E thuộc đường thẳng BC với hoành độ điểm E bằng 90
+ Ta có: \(B\left( {150;150} \right),C\left( {0;250} \right) \Rightarrow \overrightarrow {BC} = \left( { – 150;100} \right) \Rightarrow \overrightarrow {{n_{BC}}} = \left( {100;150} \right)\)
+ Phương trình đường thẳng BC là: \(100\left( {x – 0} \right) + 150\left( {y – 250} \right) = 0 \Rightarrow 2x + 3y – 750 = 0\)
+ Điểm E thuộc đường thẳng BC có hoành độ bằng 90 nên tung độ của E là 190
+ Do 183 cm < 190 cm nên bố mẹ bạn Nam có thể kê chiếc tủ lạnh có bề ngang là 90 cm và chiều cao là 183 cm.
GIẢI SBT Toán 10 Kết nối tri thức Chương 7 Bài 19
=========
THUỘC: Giải sách bài tập toán 10 – Kết nối
